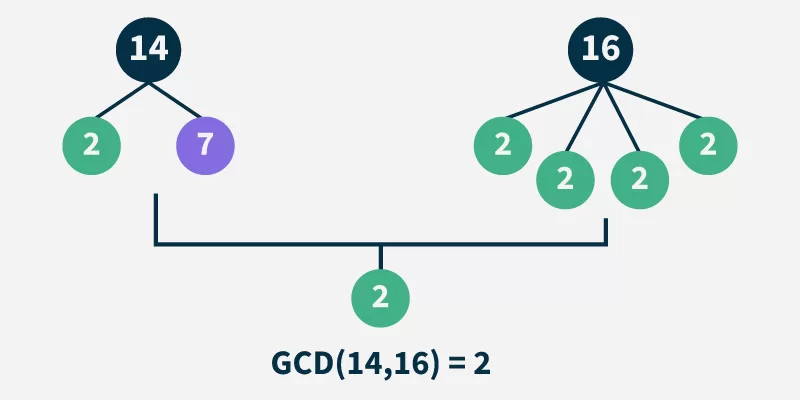
GCD Greatest Common Divisor: Euclidean Algorithm Explained

What is GCD (Greatest Common Divisor)?

Simple. The GCD Greatest Common Divisor of two or more integers is the largest integer that divides all of them evenly (with zero remainder).

Examples:

GCD of 20 and 30 is 10 — because 10 is the largest that divides both without remainder.
GCD of 42, 120, and 285 is 3.

Why does GCD matter? Well — from simplifying fractions to cryptography to scheduling problems — knowing the GCD can make things simpler, faster, cleaner.

Why the Euclidean Algorithm?

You could find GCD by listing all divisors and picking the largest common one — but that’s painful, especially with big numbers.

Instead, the Euclidean Algorithm offers a clever shortcut. It uses this really neat property:

gcd(a, b) = gcd(b, a % b) — you replace the bigger number with its remainder when divided by the smaller one, and repeat.

You keep doing that until one of the numbers becomes zero; the other number is the GCD. Super quick. Super efficient.

It’s one of the oldest algorithms in mathematics (yes — seriously ancient 🙃), but still one of the most useful.

Euclidean Algorithm — Walkthrough (with an Example)

Let me show you how it works with 48 and 18 — I like small numbers for clarity.

Start: a = 48, b = 18
Compute a % b → 48 % 18 = 12
Replace: a = 18, b = 12
Compute a % b → 18 % 12 = 6
Replace: a = 12, b = 6
Compute a % b → 12 % 6 = 0
Since remainder is zero, stop. GCD = 6

Instead of checking every possible divisor, you get to the result in a few steps.

GCD + Euclidean Algorithm in C++ & Java — Code You Can Use

Here’s clean, no-BS code that you can copy-paste and play with.

C++ Implementation

#include <iostream>
using namespace std;

int gcd(int a, int b) {
    while (b != 0) {
        int temp = b;
        b = a % b;
        a = temp;
    }
    return a;
}

int main() {
    int num1, num2;
    cout << "Enter two numbers: ";
    cin >> num1 >> num2;
    cout << "GCD Greatest Common Divisor is: " << gcd(num1, num2) << endl;
    return 0;
}

cpp

Java Implementation

import java.util.Scanner;

public class Main {
    public static int gcd(int a, int b) {
        while (b != 0) {
            int temp = b;
            b = a % b;
            a = temp;
        }
        return a;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        System.out.print("Enter two numbers: ");
        int num1 = sc.nextInt();
        int num2 = sc.nextInt();
        System.out.println("GCD Greatest Common Divisor is: "   gcd(num1, num2));
    }
}

java

Both follow the exact Euclidean logic. Clean. Fast.

If you like, you can even write a recursive version — one-liner-style:

int gcd(int a, int b) {
    return (b == 0) ? a : gcd(b, a % b);
}

java

When & Where We Use GCD and the Euclidean Algorithm — Real World Stuff

This isn’t just abstract math. I’ve seen GCD Greatest Common Divisor show up when:

🧮 Reducing fractions to simplest form (like simplifying ratios, or fractions in math classes)
🔐 Cryptography & security algorithms (lots of number-theory stuff under the hood) — you need to check if two numbers are “coprime” (i.e. their GCD = 1)
📐 Working with ratios (say, resizing images, scaling dimensions, managing proportions)
💡 Algorithmic problems (when you need to find common denominators, LCM, or optimize something across two or more numbers)

Honestly — once you know GCD and the Euclidean Algorithm, you start noticing them popping up in surprising places.

What About More Than Two Numbers?

Good question. If you have more than two numbers (say a, b, c, d, …), you can still do this:

GCD(a, b, c, d, …) = GCD( GCD( GCD(a, b), c ), d, … )

Compute GCD of first two, then use that result with the next number, and so on. Works like a charm.

Advanced: Extensions & Variants (Heads-Up for Big Numbers or Extra Use Cases)

There’s a variant called Binary GCD algorithm (also known as Stein’s algorithm) that avoids modulo entirely — uses bitwise operations. Might be useful if you’re doing very low-level optimizations.
If you want not only GCD but also numbers x, y such that a·x + b·y = gcd(a, b), that’s possible via the Extended Euclidean Algorithm. Useful in cryptography (modular inverses etc).

How the Euclidean Algorithm Works (With a Simple Example)

Let’s find the GCD Greatest Common Divisor of 48 and 18.

Step	a	b	a % b (remainder)
1	48	18	48 % 18 = 12
2	18	12	18 % 12 = 6
3	12	6	12 % 6 = 0

Stop when remainder becomes 0.

👉 GCD = 6

Final Thoughts:

When I first learned about the Euclidean Algorithm, I honestly thought:
“That’s it? This tiny logic solves such a massive problem?”

And that’s the beauty of algorithms — simple ideas solving complex problems.

If you’re preparing for software engineering interviews, competitive programming, cybersecurity, or just want to build a strong foundation in problem-solving, understanding the GCD Greatest Common Divisor and Euclidean Algorithm isn’t just helpful — it’s essential.

Kaashiv Infotech Offers, Full Stack Python Course, Data Science Course, & More, visit their website www.kaashivinfotech.com.