If you’ve ever stared at a quadratic equation during an exam or while debugging some math-heavy code and thought, “There must be a shortcut,” you’re right. The sum and product of roots method is that shortcut. Instead of solving equations step by step, you can read hidden information directly from the coefficients.
It sounds almost like cheating, but it isn’t. It’s pure mathematics, and it’s been around since the 16th century—thanks to a brilliant French mathematician named François Viète.
In this guide, you’ll learn:
- How to quickly find the sum of roots of quadratic equations and higher-degree equations.
- How to get the product of roots just as easily.
- Real-world applications in coding, competitive exams, and algorithm design.
- A short history lesson on Vieta’s Formula and why it still matters today.
Key Highlights
- Sum and product of roots save time in exams and coding tasks.
- Works for quadratic, cubic, and even 4th-degree (quartic) equations.
- Used in symbolic computation libraries (like Python’s SymPy).
- François Viète introduced the idea in the late 1500s.
- Shortcut formulas can eliminate solving altogether.
1. Sum of Roots of Quadratic Equation (Formula & Example)
Let’s start with the classic:
A quadratic equation looks like this:

The roots (solutions) are usually found with the quadratic formula. But if all you need is the sum of roots, here’s the trick:
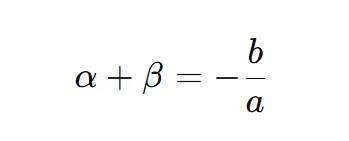
👉 That’s the sum of roots of a quadratic equation. No solving. Just coefficients.
Example:
Equation: 2x² + 5x + 3 = 0
- Here, a = 2, b = 5, c = 3
- Sum of roots = -b/a = -5/2
Done. No quadratic formula.
💡 Developer insight: In Python’s SymPy, this relation is hardcoded. If you run Poly(x**2 + 5*x + 3).all_coeffs(), you’ll see how coefficients are structured to represent roots indirectly. That’s Vieta’s Formula in action under the hood.
2. Product of Roots of Quadratic Equation
Equally useful is the product of roots of quadratic equation:
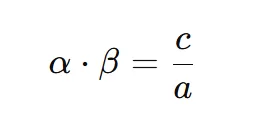
Example:
Equation: 2x² + 5x + 3 = 0
- Product = c/a = 3/2
✅ Quick and painless.
Best Practice
- Watch the signs. Many students drop marks in exams by forgetting the minus in -b/a or misplacing the denominator.
3. Sum of Roots of Cubic Equation
Now things get interesting. A cubic equation:

has three roots: α, β, γ.
The formula for the sum of roots of cubic equation:
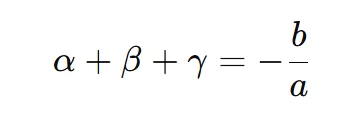
Yes—it’s the same pattern.
Example:
Equation: x³ – 6x² + 11x – 6 = 0
- a = 1, b = -6
- Sum of roots = -(-6)/1 = 6
And indeed, the roots (1, 2, 3) add up to 6.
💡 Coding relevance: Many polynomial-solving algorithms in machine learning libraries (like scikit-learn preprocessing polynomials) rely on this relationship to quickly validate results.
4. Product of Roots of Cubic Equation
For a cubic, the product of roots isn’t c/a—it’s:
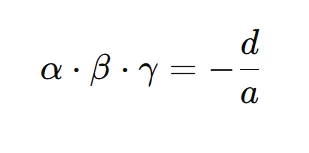
Example:
Equation: x³ – 6x² + 11x – 6 = 0
- a = 1, d = -6
- Product = -(-6)/1 = 6
Matches the roots: 1 × 2 × 3 = 6.
5. Sum and Product of Roots of 4 Degree Equation (Quartic)
Quartic equations (degree 4) look scary, but the same idea applies.
For:
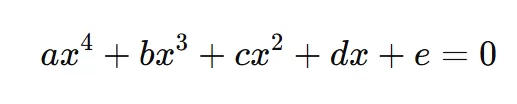
with roots α, β, γ, δ:
- Sum of roots of 4 degree equation:

- Product of roots of 4 degree equation:
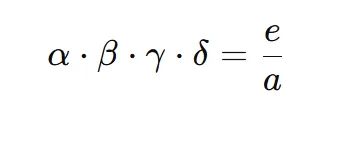
Example:
Equation: x⁴ – 10x³ + 35x² – 50x + 24 = 0
- a = 1, b = -10, e = 24
- Sum = -(-10)/1 = 10
- Product = 24/1 = 24
And indeed, the roots (1, 2, 3, 4) add up to 10 and multiply to 24.
💡 Real-world use: Quartics show up in signal processing and cryptography. Engineers often rely on Vieta’s shortcut instead of brute-force solving to validate coefficients when working with error-correcting codes.
6. General Formula (Vieta’s Relationships for Any Degree)
Here’s the full picture:
For a polynomial:
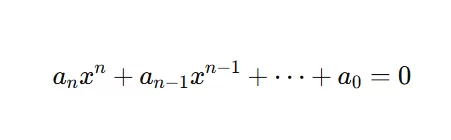
with roots r₁, r₂, …, rₙ:
- Sum of roots: -aₙ₋₁ / aₙ
- Sum of products of roots taken two at a time: aₙ₋₂ / aₙ
- Sum of products taken three at a time: -aₙ₋₃ / aₙ
- Product of roots: (-1)ⁿ * a₀ / aₙ
This is the generalized cubic polynomial formula sum and product of roots, quartic, or even nth degree case.
Quick Table
| Degree | Equation | Sum of Roots | Product of Roots |
|---|---|---|---|
| Quadratic | ax²+bx+c=0 | -b/a | c/a |
| Cubic | ax³+bx²+cx+d=0 | -b/a | -d/a |
| Quartic | ax⁴+bx³+cx²+dx+e=0 | -b/a | e/a |
7. Applications of Sum and Product of Roots
So why bother learning these shortcuts instead of just solving?
- Competitive Exams (JEE/NEET, SAT, Olympiads): Around 2–3 questions per JEE paper test direct application of sum and product of roots. Saves precious minutes.
- Coding & Algorithms: Symbolic math solvers (like MATLAB or SymPy) internally use these identities for performance optimization.
- Problem Formulation: If you know the sum and product of roots, you can reconstruct the entire quadratic or cubic equation without solving it.
Example Use Case
You’re told: “The sum of roots is 7 and the product is 10.”
→ Equation is x² – 7x + 10 = 0.
Roots? 5 and 2. Easy.
8. Vieta’s Formula and François Viète – The Backstory
It’s worth pausing to give credit where it’s due.
François Viète (1540–1603) wasn’t just another mathematician—he was one of the first to use letters to represent unknowns and coefficients systematically. Before him, equations were written almost like prose.
He developed what we now call Vieta’s Formula, showing how roots and coefficients are linked. His work laid the foundation for algebraic notation, influencing Newton, Descartes, and even modern-day coding practices.
💡 Fun fact: Viète also cracked complex ciphers for the French government using his algebraic skills—a 16th-century version of cryptography.
So the next time you use the sum and product of roots formula, remember—it’s not just a hack. It’s history.
9. Conclusion
The sum and product of roots shortcut is more than just a math trick. It’s a time-saver in exams, a validator in coding, and a piece of history in algebra.
Here’s the big takeaway:
- For quadratics, use -b/a and c/a.
- For cubics, use -b/a and -d/a.
- For quartics, use -b/a and e/a.
And if you’re ambitious, Vieta’s general formula covers any degree.
If you’re studying for exams, solving problems in code, or just exploring math for fun, remember: sometimes the fastest solutions are centuries old. Viète figured that out in the 1500s. Now it’s your turn to use it wisely.
Related Reads
- What is BODMAS Rule in Programming, AI and IT – 2025 Guide — Clear explanation of operation precedence (useful when working with expressions & roots).
- AM/PM Full Form & Meaning | 24-Hour Clock Converter & Time Chart (2025 Guide) — Great read for time‐format clarity in software & scheduling.
- Cut Copy Paste Made Easy: CTRL + C, CTRL + X, CTRL + V Shortcuts for Windows & Mac (2025 Guide) — Productivity tips that help save time, whether you’re coding or writing.
- First Generation of Computer (1940s–1950s): Year, Technology, Examples, Advantages & Disadvantages (2025 Guide) — Historical perspective if you like seeing how foundational math & logic tools evolved.
- Master Fibonacci Series in Java: Programs & Tips (2025) — Another algorithmic/control-flow topic; good for those interested in roots, recursion, and series.







