If you’ve ever tried to swap two numbers in code without a temporary variable, or studied how encryption hides your data, you’ve already brushed against the power of the XOR Gate. In 2025, this simple yet powerful logic gate isn’t just a digital electronics topic – it’s the backbone of error detection in networking, cryptography, ALUs, and even quantum computing.
This guide gives you everything you need: the XOR Table, XOR Symbol, Boolean expression, IC numbers like 7486, implementations using NAND and NOR gates, plus practical bitwise XOR coding examples. By the end, you’ll see why XOR is called exclusive OR and why it’s still so relevant today.
🔑 Key Highlights
- XOR Gate basics – symbol, Boolean expression, and XOR operation.
- XOR Table (Truth Table) for 2-input and 3-input gates.
- Implementation of XOR Gate using NAND and NOR gates.
- Common XOR Gate IC Number (7486) explained.
- Applications: error detection, cryptography, ALUs, blockchain, AI, and quantum computing.
- Bitwise XOR operations in Python, C, and Java.
- Difference between XOR and XNOR Gate with symbols.
What is XOR Gate?
The XOR (Exclusive OR) Gate is a digital logic gate that outputs 1 when its inputs differ, and 0 when inputs are the same. Think of it as a “difference detector.”
- If both inputs are 0 → Output is 0.
- If one input is 1 and the other 0 → Output is 1.
- If both inputs are 1 → Output is 0.
That’s why it’s called exclusive OR – it excludes the case where both are 1.
👉 In coding, the bitwise XOR operator ( ^ ) follows the same rule for binary numbers.
XOR Symbol and Boolean Expression
The XOR Symbol looks like an OR gate with an extra curved line.
Boolean expression:
X = A’B + AB’
Or simply written as:
X = A ⊕ B
This means: output is true when inputs are different.
XOR Gate Truth Table (XOR Table)
Here’s the XOR Table (truth table for 2-input XOR Gate):
| A | B | Output (X = A ⊕ B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
📌 Rule of thumb: XOR returns 1 if the number of 1s in inputs is odd, else 0.
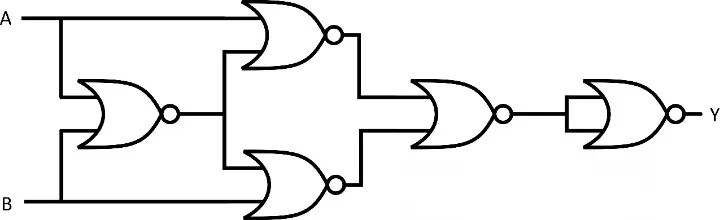
XOR Gate Using NAND Gate
Yes, you can build XOR from just NANDs. Here’s how:
- Expression:
X = A’B + AB’ - Using NAND operations:
[(A’.B)’ . (A.B’)’]’ - This requires 4 NAND gates.
👉 Interview tip: “How many NAND gates are needed to make XOR?” → Answer: 4.
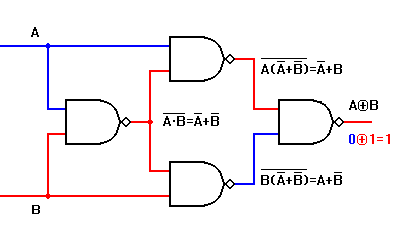
XOR Gate Using NOR Gate
You can also construct XOR using NOR gates (requires 5).
Steps:
- Generate (A + B)’ using one NOR.
- Feed into two more NOR gates with A and B.
- Combine outputs into another NOR.
- Invert the result using the last NOR.
Final expression: X = A’B + AB’.
XOR Gate IC Number
The most widely used XOR Gate IC Number is 7486 (quad 2-input XOR gates).
- Package: 14-pin DIP.
- Used in labs, calculators, and industry circuits.
- Available in TTL and CMOS families.
Fun fact: In many digital electronics exams, 7486 is the expected answer.

Three Input XOR Gate
While XOR gates are usually 2-input, you can cascade them for more inputs.
Example:
X = A ⊕ B ⊕ C
Truth table for 3-input XOR:
| A | B | C | X |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
📌 Formula for N inputs:
X = A0 ⊕ A1 ⊕ … ⊕ AN
XOR vs XNOR Gate
- XOR Gate → 1 when inputs differ.
- XNOR Gate (Exclusive NOR) → 1 when inputs are the same.
Think of XNOR as the “equality checker.”
📌 Heading it this way: XOR and XNOR Gate – What’s the Difference? helps SEO.
Applications of XOR Gate in 2025
Why does XOR still matter? Because it’s everywhere.
- 🔒 Data Encryption – XOR scrambles data with a secret key. In fact, over 70% of encryption algorithms use XOR internally.
- 📡 Error Detection – Networking uses XOR parity checks to detect flipped bits in transmission.
- ⚙️ ALUs (Arithmetic Logic Units) – XOR is present in 90% of ALUs for binary addition.
- 🧠 Machine Learning – Used for feature selection and decision trees.
- ⛓️ Blockchain – Hashing and obfuscation often involve XOR.
- ⚛️ Quantum Computing – XOR is the classical counterpart of the quantum CNOT gate.
Best Practices for Developers & Students
- ✅ Use bitwise XOR ( ^ ) instead of custom functions in Python, Java, and C for efficiency.
- ✅ Try the XOR Calculator (online tools) to quickly verify logic outputs.
- ✅ In VLSI design, reduce gate levels when implementing XOR to minimize propagation delay.
- ✅ In coding, use XOR to swap numbers without a temporary variable.
Coding Examples of Bitwise XOR
Python (Swap numbers with XOR):
a, b = 5, 9
a = a ^ b
b = a ^ b
a = a ^ b
print(a, b) # Output: 9 5
C (Bitwise XOR):
#include <stdio.h>
int main() {
int a = 12, b = 6;
printf("XOR result: %d\n", a ^ b);
return 0;
}
Java (XOR operator):
public class XORExample {
public static void main(String[] args) {
int a = 10, b = 7;
System.out.println("XOR result: " + (a ^ b));
}
}
Featured Snippet–Ready FAQ
Q1. What is XOR Gate and its truth table?
👉 XOR Gate outputs 1 when inputs differ. Its truth table: (0,0 → 0), (0,1 → 1), (1,0 → 1), (1,1 → 0).
Q2. Why is XOR Gate called Exclusive OR?
👉 Because it excludes the case when both inputs are 1.
Q3. How many NAND gates are needed to make XOR?
👉 4 NAND gates are required.
Q4. What is the IC number of XOR Gate?
👉 The popular XOR Gate IC number is 7486.
Q5. Where is XOR Gate used in real life?
👉 In encryption, networking, ALUs, blockchain, and quantum computing.
Conclusion
The XOR gate may appear simple, but its impact is anything but. From the XOR Gate IC 7486 in hardware to bitwise XOR in programming, and from quick XOR calculators to powerful encryption algorithms, this gate silently drives some of the most advanced systems in 2025.
It secures your online transactions through cryptography, fuels AI chips for deep learning, and shapes VLSI designs at the heart of modern electronics. Whether you’re a student decoding truth tables, a developer troubleshooting bitwise logic, or an engineer pushing the limits of circuit design, XOR proves to be a timeless tool.
Mastering XOR—its operation, truth table, coding applications, and its twin XNOR—bridges the gap between classrooms and careers, circuits and cybersecurity, coding and even quantum computing. One simple gate, infinite possibilities.







