Given an undirected and unweighted graph, find the smallest cut (smallest number of edges that disconnects the graph into two components).
The input graph may have parallel edges.
For example consider the following example, the smallest cut has 2 edges.
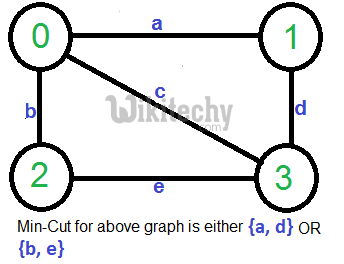
A Simple Solution use Max-Flow based s-t cut algorithm to find minimum cut. Consider every pair of vertices as source ‘s’ and sink ‘t’, and call minimum s-t cut algorithm to find the s-t cut. Return minimum of all s-t cuts. Best possible time complexity of this algorithm is O(V5) for a graph. [How? there are total possible V2 pairs and s-t cut algorithm for one pair takes O(V*E) time and E = O(V2)].
[ad type=”banner”]Below is simple Karger’s Algorithm for this purpose. Below Karger’s algorithm can be implemented in O(E) = O(V2) time.
1) Initialize contracted graph CG as copy of original graph
2) While there are more than 2 vertices.
a) Pick a random edge (u, v) in the contracted graph.
b) Merge (or contract) u and v into a single vertex (update
the contracted graph).
c) Remove self-loops
3) Return cut represented by two vertices.
Let us understand above algorithm through the example given.
Let the first randomly picked vertex be ‘a‘ which connects vertices 0 and 1. We remove this edge and contract the graph (combine vertices 0 and 1). We get the following graph.
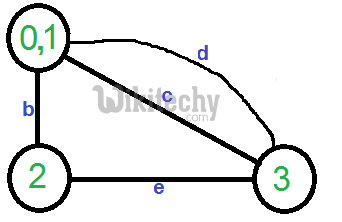
Let the next randomly picked edge be ‘d’. We remove this edge and combine vertices (0,1) and 3.
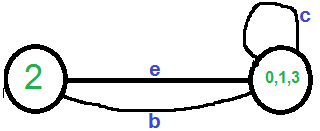
We need to remove self-loops in the graph. So we remove edge ‘c’

Now graph has two vertices, so we stop. The number of edges in the resultant graph is the cut produced by Karger’s algorithm.
Karger’s algorithm is a Monte Carlo algorithm and cut produced by it may not be minimum.
For example, the following diagram shows that a different order of picking random edges produces a min-cut of size 3.

Below is C++ implementation of above algorithm. The input graph is represented as a collection of edges and union-find data structure is used to keep track of components.
[pastacode lang=”cpp” manual=”%2F%2F%20Karger’s%20algorithm%20to%20find%20Minimum%20Cut%20in%20an%0A%2F%2F%20undirected%2C%20unweighted%20and%20connected%20graph.%0A%23include%20%3Cstdio.h%3E%0A%23include%20%3Cstdlib.h%3E%0A%23include%20%3Ctime.h%3E%0A%20%0A%2F%2F%20a%20structure%20to%20represent%20a%20unweighted%20edge%20in%20graph%0Astruct%20Edge%0A%7B%0A%20%20%20%20int%20src%2C%20dest%3B%0A%7D%3B%0A%20%0A%2F%2F%20a%20structure%20to%20represent%20a%20connected%2C%20undirected%0A%2F%2F%20and%20unweighted%20graph%20as%20a%20collection%20of%20edges.%0Astruct%20Graph%0A%7B%0A%20%20%20%20%2F%2F%20V-%3E%20Number%20of%20vertices%2C%20E-%3E%20Number%20of%20edges%0A%20%20%20%20int%20V%2C%20E%3B%0A%20%0A%20%20%20%20%2F%2F%20graph%20is%20represented%20as%20an%20array%20of%20edges.%0A%20%20%20%20%2F%2F%20Since%20the%20graph%20is%20undirected%2C%20the%20edge%0A%20%20%20%20%2F%2F%20from%20src%20to%20dest%20is%20also%20edge%20from%20dest%0A%20%20%20%20%2F%2F%20to%20src.%20Both%20are%20counted%20as%201%20edge%20here.%0A%20%20%20%20Edge*%20edge%3B%0A%7D%3B%0A%20%0A%2F%2F%20A%20structure%20to%20represent%20a%20subset%20for%20union-find%0Astruct%20subset%0A%7B%0A%20%20%20%20int%20parent%3B%0A%20%20%20%20int%20rank%3B%0A%7D%3B%0A%20%0A%2F%2F%20Function%20prototypes%20for%20union-find%20(These%20functions%20are%20defined%0A%2F%2F%20after%20kargerMinCut()%20)%0Aint%20find(struct%20subset%20subsets%5B%5D%2C%20int%20i)%3B%0Avoid%20Union(struct%20subset%20subsets%5B%5D%2C%20int%20x%2C%20int%20y)%3B%0A%20%0A%2F%2F%20A%20very%20basic%20implementation%20of%20Karger’s%20randomized%0A%2F%2F%20algorithm%20for%20finding%20the%20minimum%20cut.%20Please%20note%0A%2F%2F%20that%20Karger’s%20algorithm%20is%20a%20Monte%20Carlo%20Randomized%20algo%0A%2F%2F%20and%20the%20cut%20returned%20by%20the%20algorithm%20may%20not%20be%0A%2F%2F%20minimum%20always%0Aint%20kargerMinCut(struct%20Graph*%20graph)%0A%7B%0A%20%20%20%20%2F%2F%20Get%20data%20of%20given%20graph%0A%20%20%20%20int%20V%20%3D%20graph-%3EV%2C%20E%20%3D%20graph-%3EE%3B%0A%20%20%20%20Edge%20*edge%20%3D%20graph-%3Eedge%3B%0A%20%0A%20%20%20%20%2F%2F%20Allocate%20memory%20for%20creating%20V%20subsets.%0A%20%20%20%20struct%20subset%20*subsets%20%3D%20new%20subset%5BV%5D%3B%0A%20%0A%20%20%20%20%2F%2F%20Create%20V%20subsets%20with%20single%20elements%0A%20%20%20%20for%20(int%20v%20%3D%200%3B%20v%20%3C%20V%3B%20%2B%2Bv)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20subsets%5Bv%5D.parent%20%3D%20v%3B%0A%20%20%20%20%20%20%20%20subsets%5Bv%5D.rank%20%3D%200%3B%0A%20%20%20%20%7D%0A%20%0A%20%20%20%20%2F%2F%20Initially%20there%20are%20V%20vertices%20in%0A%20%20%20%20%2F%2F%20contracted%20graph%0A%20%20%20%20int%20vertices%20%3D%20V%3B%0A%20%0A%20%20%20%20%2F%2F%20Keep%20contracting%20vertices%20until%20there%20are%0A%20%20%20%20%2F%2F%202%20vertices.%0A%20%20%20%20while%20(vertices%20%3E%202)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%2F%2F%20Pick%20a%20random%20edge%0A%20%20%20%20%20%20%20int%20i%20%3D%20rand()%20%25%20E%3B%0A%20%0A%20%20%20%20%20%20%20%2F%2F%20Find%20vertices%20(or%20sets)%20of%20two%20corners%0A%20%20%20%20%20%20%20%2F%2F%20of%20current%20edge%0A%20%20%20%20%20%20%20int%20subset1%20%3D%20find(subsets%2C%20edge%5Bi%5D.src)%3B%0A%20%20%20%20%20%20%20int%20subset2%20%3D%20find(subsets%2C%20edge%5Bi%5D.dest)%3B%0A%20%0A%20%20%20%20%20%20%20%2F%2F%20If%20two%20corners%20belong%20to%20same%20subset%2C%0A%20%20%20%20%20%20%20%2F%2F%20then%20no%20point%20considering%20this%20edge%0A%20%20%20%20%20%20%20if%20(subset1%20%3D%3D%20subset2)%0A%20%20%20%20%20%20%20%20%20continue%3B%0A%20%0A%20%20%20%20%20%20%20%2F%2F%20Else%20contract%20the%20edge%20(or%20combine%20the%0A%20%20%20%20%20%20%20%2F%2F%20corners%20of%20edge%20into%20one%20vertex)%0A%20%20%20%20%20%20%20else%0A%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20printf(%22Contracting%20edge%20%25d-%25d%5Cn%22%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20edge%5Bi%5D.src%2C%20edge%5Bi%5D.dest)%3B%0A%20%20%20%20%20%20%20%20%20%20vertices–%3B%0A%20%20%20%20%20%20%20%20%20%20Union(subsets%2C%20subset1%2C%20subset2)%3B%0A%20%20%20%20%20%20%20%7D%0A%20%20%20%20%7D%0A%20%0A%20%20%20%20%2F%2F%20Now%20we%20have%20two%20vertices%20(or%20subsets)%20left%20in%0A%20%20%20%20%2F%2F%20the%20contracted%20graph%2C%20so%20count%20the%20edges%20between%0A%20%20%20%20%2F%2F%20two%20components%20and%20return%20the%20count.%0A%20%20%20%20int%20cutedges%20%3D%200%3B%0A%20%20%20%20for%20(int%20i%3D0%3B%20i%3CE%3B%20i%2B%2B)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20int%20subset1%20%3D%20find(subsets%2C%20edge%5Bi%5D.src)%3B%0A%20%20%20%20%20%20%20%20int%20subset2%20%3D%20find(subsets%2C%20edge%5Bi%5D.dest)%3B%0A%20%20%20%20%20%20%20%20if%20(subset1%20!%3D%20subset2)%0A%20%20%20%20%20%20%20%20%20%20cutedges%2B%2B%3B%0A%20%20%20%20%7D%0A%20%0A%20%20%20%20return%20cutedges%3B%0A%7D%0A%20%0A%2F%2F%20A%20utility%20function%20to%20find%20set%20of%20an%20element%20i%0A%2F%2F%20(uses%20path%20compression%20technique)%0Aint%20find(struct%20subset%20subsets%5B%5D%2C%20int%20i)%0A%7B%0A%20%20%20%20%2F%2F%20find%20root%20and%20make%20root%20as%20parent%20of%20i%0A%20%20%20%20%2F%2F%20(path%20compression)%0A%20%20%20%20if%20(subsets%5Bi%5D.parent%20!%3D%20i)%0A%20%20%20%20%20%20subsets%5Bi%5D.parent%20%3D%0A%20%20%20%20%20%20%20%20%20%20%20%20%20find(subsets%2C%20subsets%5Bi%5D.parent)%3B%0A%20%0A%20%20%20%20return%20subsets%5Bi%5D.parent%3B%0A%7D%0A%20%0A%2F%2F%20A%20function%20that%20does%20union%20of%20two%20sets%20of%20x%20and%20y%0A%2F%2F%20(uses%20union%20by%20rank)%0Avoid%20Union(struct%20subset%20subsets%5B%5D%2C%20int%20x%2C%20int%20y)%0A%7B%0A%20%20%20%20int%20xroot%20%3D%20find(subsets%2C%20x)%3B%0A%20%20%20%20int%20yroot%20%3D%20find(subsets%2C%20y)%3B%0A%20%0A%20%20%20%20%2F%2F%20Attach%20smaller%20rank%20tree%20under%20root%20of%20high%0A%20%20%20%20%2F%2F%20rank%20tree%20(Union%20by%20Rank)%0A%20%20%20%20if%20(subsets%5Bxroot%5D.rank%20%3C%20subsets%5Byroot%5D.rank)%0A%20%20%20%20%20%20%20%20subsets%5Bxroot%5D.parent%20%3D%20yroot%3B%0A%20%20%20%20else%20if%20(subsets%5Bxroot%5D.rank%20%3E%20subsets%5Byroot%5D.rank)%0A%20%20%20%20%20%20%20%20subsets%5Byroot%5D.parent%20%3D%20xroot%3B%0A%20%0A%20%20%20%20%2F%2F%20If%20ranks%20are%20same%2C%20then%20make%20one%20as%20root%20and%0A%20%20%20%20%2F%2F%20increment%20its%20rank%20by%20one%0A%20%20%20%20else%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20subsets%5Byroot%5D.parent%20%3D%20xroot%3B%0A%20%20%20%20%20%20%20%20subsets%5Bxroot%5D.rank%2B%2B%3B%0A%20%20%20%20%7D%0A%7D%0A%20%0A%2F%2F%20Creates%20a%20graph%20with%20V%20vertices%20and%20E%20edges%0Astruct%20Graph*%20createGraph(int%20V%2C%20int%20E)%0A%7B%0A%20%20%20%20Graph*%20graph%20%3D%20new%20Graph%3B%0A%20%20%20%20graph-%3EV%20%3D%20V%3B%0A%20%20%20%20graph-%3EE%20%3D%20E%3B%0A%20%20%20%20graph-%3Eedge%20%3D%20new%20Edge%5BE%5D%3B%0A%20%20%20%20return%20graph%3B%0A%7D%0A%20%0A%2F%2F%20Driver%20program%20to%20test%20above%20functions%0Aint%20main()%0A%7B%0A%20%20%20%20%2F*%20Let%20us%20create%20following%20unweighted%20graph%0A%20%20%20%20%20%20%20%200——1%0A%20%20%20%20%20%20%20%20%7C%20%5C%20%20%20%20%7C%0A%20%20%20%20%20%20%20%20%7C%20%20%20%5C%20%20%7C%0A%20%20%20%20%20%20%20%20%7C%20%20%20%20%20%5C%7C%0A%20%20%20%20%20%20%20%202——3%20%20%20*%2F%0A%20%20%20%20int%20V%20%3D%204%3B%20%20%2F%2F%20Number%20of%20vertices%20in%20graph%0A%20%20%20%20int%20E%20%3D%205%3B%20%20%2F%2F%20Number%20of%20edges%20in%20graph%0A%20%20%20%20struct%20Graph*%20graph%20%3D%20createGraph(V%2C%20E)%3B%0A%20%0A%20%20%20%20%2F%2F%20add%20edge%200-1%0A%20%20%20%20graph-%3Eedge%5B0%5D.src%20%3D%200%3B%0A%20%20%20%20graph-%3Eedge%5B0%5D.dest%20%3D%201%3B%0A%20%0A%20%20%20%20%2F%2F%20add%20edge%200-2%0A%20%20%20%20graph-%3Eedge%5B1%5D.src%20%3D%200%3B%0A%20%20%20%20graph-%3Eedge%5B1%5D.dest%20%3D%202%3B%0A%20%0A%20%20%20%20%2F%2F%20add%20edge%200-3%0A%20%20%20%20graph-%3Eedge%5B2%5D.src%20%3D%200%3B%0A%20%20%20%20graph-%3Eedge%5B2%5D.dest%20%3D%203%3B%0A%20%0A%20%20%20%20%2F%2F%20add%20edge%201-3%0A%20%20%20%20graph-%3Eedge%5B3%5D.src%20%3D%201%3B%0A%20%20%20%20graph-%3Eedge%5B3%5D.dest%20%3D%203%3B%0A%20%0A%20%20%20%20%2F%2F%20add%20edge%202-3%0A%20%20%20%20graph-%3Eedge%5B4%5D.src%20%3D%202%3B%0A%20%20%20%20graph-%3Eedge%5B4%5D.dest%20%3D%203%3B%0A%20%0A%20%20%20%20%2F%2F%20Use%20a%20different%20seed%20value%20for%20every%20run.%0A%20%20%20%20srand(time(NULL))%3B%0A%20%0A%20%20%20%20printf(%22%5CnCut%20found%20by%20Karger’s%20randomized%20algo%20is%20%25d%5Cn%22%2C%0A%20%20%20%20%20%20%20%20%20%20%20kargerMinCut(graph))%3B%0A%20%0A%20%20%20%20return%200%3B%0A%7D” message=”C++ Program” highlight=”” provider=”manual”/]Output:
Contracting edge 0-2 Contracting edge 0-3 Cut found by Karger's randomized algo is 2
Note that the above program is based on outcome of a random function and may produce different output.
In this post, we have discussed simple Karger’s algorithm and have seen that the algorithm doesn’t always produce min-cut. The above algorithm produces min-cut with probability greater or equal to that 1/(n2).
[ad type=”banner”]