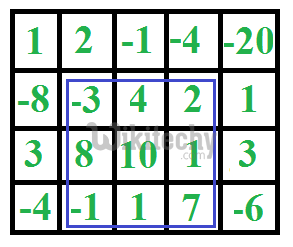
Given a 2D array, find the maximum sum subarray in it. For example, in the following 2D array, the maximum sum subarray is highlighted with blue rectangle and sum of this subarray is 29.
This problem is mainly an extension of Largest Sum Contiguous Subarray for 1D array.
The naive solution for this problem is to check every possible rectangle in given 2D array. This solution requires 4 nested loops and time complexity of this solution would be O(n^4).
[ad type=”banner”]Kadane’s algorithm for 1D array can be used to reduce the time complexity to O(n^3). The idea is to fix the left and right columns one by one and find the maximum sum contiguous rows for every left and right column pair. We basically find top and bottom row numbers (which have maximum sum) for every fixed left and right column pair. To find the top and bottom row numbers, calculate sun of elements in every row from left to right and store these sums in an array say temp[]. So temp[i] indicates sum of elements from left to right in row i. If we apply Kadane’s 1D algorithm on temp[], and get the maximum sum subarray of temp, this maximum sum would be the maximum possible sum with left and right as boundary columns. To get the overall maximum sum, we compare this sum with the maximum sum so far.
[pastacode lang=”c” manual=”%2F%2F%20Program%20to%20find%20maximum%20sum%20subarray%20in%20a%20given%202D%20array%0A%23include%20%3Cstdio.h%3E%0A%23include%20%3Cstring.h%3E%0A%23include%20%3Climits.h%3E%0A%23define%20ROW%204%0A%23define%20COL%205%0A%20%0A%2F%2F%20Implementation%20of%20Kadane’s%20algorithm%20for%201D%20array.%20The%20function%20%0A%2F%2F%20returns%20the%20maximum%20sum%20and%20stores%20starting%20and%20ending%20indexes%20of%20the%20%0A%2F%2F%20maximum%20sum%20subarray%20at%20addresses%20pointed%20by%20start%20and%20finish%20pointers%20%0A%2F%2F%20respectively.%0Aint%20kadane(int*%20arr%2C%20int*%20start%2C%20int*%20finish%2C%20int%20n)%0A%7B%0A%20%20%20%20%2F%2F%20initialize%20sum%2C%20maxSum%20and%0A%20%20%20%20int%20sum%20%3D%200%2C%20maxSum%20%3D%20INT_MIN%2C%20i%3B%0A%20%0A%20%20%20%20%2F%2F%20Just%20some%20initial%20value%20to%20check%20for%20all%20negative%20values%20case%0A%20%20%20%20*finish%20%3D%20-1%3B%0A%20%0A%20%20%20%20%2F%2F%20local%20variable%0A%20%20%20%20int%20local_start%20%3D%200%3B%0A%20%0A%20%20%20%20for%20(i%20%3D%200%3B%20i%20%3C%20n%3B%20%2B%2Bi)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20sum%20%2B%3D%20arr%5Bi%5D%3B%0A%20%20%20%20%20%20%20%20if%20(sum%20%3C%200)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20sum%20%3D%200%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20local_start%20%3D%20i%2B1%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20else%20if%20(sum%20%3E%20maxSum)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20maxSum%20%3D%20sum%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20*start%20%3D%20local_start%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20*finish%20%3D%20i%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%7D%0A%20%0A%20%20%20%20%20%2F%2F%20There%20is%20at-least%20one%20non-negative%20number%0A%20%20%20%20if%20(*finish%20!%3D%20-1)%0A%20%20%20%20%20%20%20%20return%20maxSum%3B%0A%20%0A%20%20%20%20%2F%2F%20Special%20Case%3A%20When%20all%20numbers%20in%20arr%5B%5D%20are%20negative%0A%20%20%20%20maxSum%20%3D%20arr%5B0%5D%3B%0A%20%20%20%20*start%20%3D%20*finish%20%3D%200%3B%0A%20%0A%20%20%20%20%2F%2F%20Find%20the%20maximum%20element%20in%20array%0A%20%20%20%20for%20(i%20%3D%201%3B%20i%20%3C%20n%3B%20i%2B%2B)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20if%20(arr%5Bi%5D%20%3E%20maxSum)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20maxSum%20%3D%20arr%5Bi%5D%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20*start%20%3D%20*finish%20%3D%20i%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%7D%0A%20%20%20%20return%20maxSum%3B%0A%7D%0A%20%0A%2F%2F%20The%20main%20function%20that%20finds%20maximum%20sum%20rectangle%20in%20M%5B%5D%5B%5D%0Avoid%20findMaxSum(int%20M%5B%5D%5BCOL%5D)%0A%7B%0A%20%20%20%20%2F%2F%20Variables%20to%20store%20the%20final%20output%0A%20%20%20%20int%20maxSum%20%3D%20INT_MIN%2C%20finalLeft%2C%20finalRight%2C%20finalTop%2C%20finalBottom%3B%0A%20%0A%20%20%20%20int%20left%2C%20right%2C%20i%3B%0A%20%20%20%20int%20temp%5BROW%5D%2C%20sum%2C%20start%2C%20finish%3B%0A%20%0A%20%20%20%20%2F%2F%20Set%20the%20left%20column%0A%20%20%20%20for%20(left%20%3D%200%3B%20left%20%3C%20COL%3B%20%2B%2Bleft)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20Initialize%20all%20elements%20of%20temp%20as%200%0A%20%20%20%20%20%20%20%20memset(temp%2C%200%2C%20sizeof(temp))%3B%0A%20%0A%20%20%20%20%20%20%20%20%2F%2F%20Set%20the%20right%20column%20for%20the%20left%20column%20set%20by%20outer%20loop%0A%20%20%20%20%20%20%20%20for%20(right%20%3D%20left%3B%20right%20%3C%20COL%3B%20%2B%2Bright)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20Calculate%20sum%20between%20current%20left%20and%20right%20for%20every%20row%20’i’%0A%20%20%20%20%20%20%20%20%20%20%20%20for%20(i%20%3D%200%3B%20i%20%3C%20ROW%3B%20%2B%2Bi)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20temp%5Bi%5D%20%2B%3D%20M%5Bi%5D%5Bright%5D%3B%0A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20Find%20the%20maximum%20sum%20subarray%20in%20temp%5B%5D.%20The%20kadane()%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20function%20also%20sets%20values%20of%20start%20and%20finish.%20%20So%20’sum’%20is%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20sum%20of%20rectangle%20between%20(start%2C%20left)%20and%20(finish%2C%20right)%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20%20which%20is%20the%20maximum%20sum%20with%20boundary%20columns%20strictly%20as%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20%20left%20and%20right.%0A%20%20%20%20%20%20%20%20%20%20%20%20sum%20%3D%20kadane(temp%2C%20%26start%2C%20%26finish%2C%20ROW)%3B%0A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20Compare%20sum%20with%20maximum%20sum%20so%20far.%20If%20sum%20is%20more%2C%20then%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20update%20maxSum%20and%20other%20output%20values%0A%20%20%20%20%20%20%20%20%20%20%20%20if%20(sum%20%3E%20maxSum)%0A%20%20%20%20%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20maxSum%20%3D%20sum%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20finalLeft%20%3D%20left%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20finalRight%20%3D%20right%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20finalTop%20%3D%20start%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20finalBottom%20%3D%20finish%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%7D%0A%20%0A%20%20%20%20%2F%2F%20Print%20final%20values%0A%20%20%20%20printf(%22(Top%2C%20Left)%20(%25d%2C%20%25d)%5Cn%22%2C%20finalTop%2C%20finalLeft)%3B%0A%20%20%20%20printf(%22(Bottom%2C%20Right)%20(%25d%2C%20%25d)%5Cn%22%2C%20finalBottom%2C%20finalRight)%3B%0A%20%20%20%20printf(%22Max%20sum%20is%3A%20%25d%5Cn%22%2C%20maxSum)%3B%0A%7D%0A%20%0A%2F%2F%20Driver%20program%20to%20test%20above%20functions%0Aint%20main()%0A%7B%0A%20%20%20%20int%20M%5BROW%5D%5BCOL%5D%20%3D%20%7B%7B1%2C%202%2C%20-1%2C%20-4%2C%20-20%7D%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7B-8%2C%20-3%2C%204%2C%202%2C%201%7D%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7B3%2C%208%2C%2010%2C%201%2C%203%7D%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7B-4%2C%20-1%2C%201%2C%207%2C%20-6%7D%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7D%3B%0A%20%0A%20%20%20%20findMaxSum(M)%3B%0A%20%0A%20%20%20%20return%200%3B%0A%7D” message=”C” highlight=”” provider=”manual”/]Output :
(Top, Left) (1, 1) (Bottom, Right) (3, 3) Max sum is: 29
Time Complexity: O(n^3)