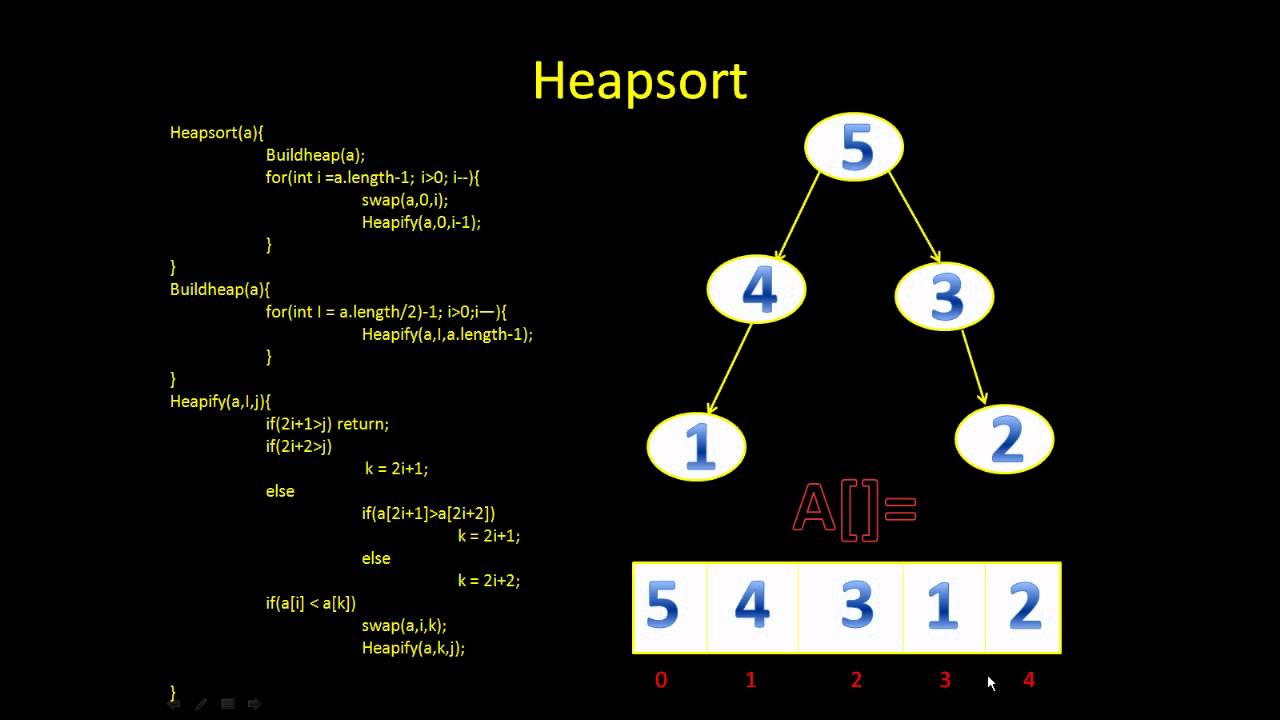
Heap sort is a comparison based sorting technique based on Binary Heap data structure. It is similar to selection sort where we first find the maximum element and place the maximum element at the end. We repeat the same process for remaining element.
What is Binary Heap?
Let us first define a Complete Binary Tree. A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible (Source Wikipedia)
A Binary Heap is a Complete Binary Tree where items are stored in a special order such that value in a parent node is greater(or smaller) than the values in its two children nodes. The former is called as max heap and the latter is called min heap. The heap can be represented by binary tree or array.
Why array based representation for Binary Heap?
Since a Binary Heap is a Complete Binary Tree, it can be easily represented as array and array based representation is space efficient. If the parent node is stored at index I, the left child can be calculated by 2 * I + 1 and right child by 2 * I + 2 (assuming the indexing starts at 0).
Heap Sort Algorithm for sorting in increasing order:
1. Build a max heap from the input data.
2. At this point, the largest item is stored at the root of the heap. Replace it with the last item of the heap followed by reducing the size of heap by 1. Finally, heapify the root of tree.
3. Repeat above steps while size of heap is greater than 1.
How to build the heap?
Heapify procedure can be applied to a node only if its children nodes are heapified. So the heapification must be performed in the bottom up order.
Lets understand with the help of an example:
Input data: 4, 10, 3, 5, 1
4(0)
/ \
10(1) 3(2)
/ \
5(3) 1(4)
The numbers in bracket represent the indices in the array
representation of data.
Applying heapify procedure to index 1:
4(0)
/ \
10(1) 3(2)
/ \
5(3) 1(4)
Applying heapify procedure to index 0:
10(0)
/ \
5(1) 3(2)
/ \
4(3) 1(4)
The heapify procedure calls itself recursively to build heap
in top down manner.
C++ programming:
[pastacode lang=”cpp” manual=”%2F%2F%20C%2B%2B%20program%20for%20implementation%20of%20Heap%20Sort%0A%23include%20%3Ciostream%3E%0Ausing%20namespace%20std%3B%0A%20%0A%2F%2F%20To%20heapify%20a%20subtree%20rooted%20with%20node%20i%20which%20is%0A%2F%2F%20an%20index%20in%20arr%5B%5D.%20n%20is%20size%20of%20heap%0Avoid%20heapify(int%20arr%5B%5D%2C%20int%20n%2C%20int%20i)%0A%7B%0A%20%20%20%20int%20largest%20%3D%20i%3B%20%20%2F%2F%20Initialize%20largest%20as%20root%0A%20%20%20%20int%20l%20%3D%202*i%20%2B%201%3B%20%20%2F%2F%20left%20%3D%202*i%20%2B%201%0A%20%20%20%20int%20r%20%3D%202*i%20%2B%202%3B%20%20%2F%2F%20right%20%3D%202*i%20%2B%202%0A%20%0A%20%20%20%20%2F%2F%20If%20left%20child%20is%20larger%20than%20root%0A%20%20%20%20if%20(l%20%3C%20n%20%26%26%20arr%5Bl%5D%20%3E%20arr%5Blargest%5D)%0A%20%20%20%20%20%20%20%20largest%20%3D%20l%3B%0A%20%0A%20%20%20%20%2F%2F%20If%20right%20child%20is%20larger%20than%20largest%20so%20far%0A%20%20%20%20if%20(r%20%3C%20n%20%26%26%20arr%5Br%5D%20%3E%20arr%5Blargest%5D)%0A%20%20%20%20%20%20%20%20largest%20%3D%20r%3B%0A%20%0A%20%20%20%20%2F%2F%20If%20largest%20is%20not%20root%0A%20%20%20%20if%20(largest%20!%3D%20i)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20swap(arr%5Bi%5D%2C%20arr%5Blargest%5D)%3B%0A%20%0A%20%20%20%20%20%20%20%20%2F%2F%20Recursively%20heapify%20the%20affected%20sub-tree%0A%20%20%20%20%20%20%20%20heapify(arr%2C%20n%2C%20largest)%3B%0A%20%20%20%20%7D%0A%7D%0A%20%0A%2F%2F%20main%20function%20to%20do%20heap%20sort%0Avoid%20heapSort(int%20arr%5B%5D%2C%20int%20n)%0A%7B%0A%20%20%20%20%2F%2F%20Build%20heap%20(rearrange%20array)%0A%20%20%20%20for%20(int%20i%20%3D%20n%20%2F%202%20-%201%3B%20i%20%3E%3D%200%3B%20i–)%0A%20%20%20%20%20%20%20%20heapify(arr%2C%20n%2C%20i)%3B%0A%20%0A%20%20%20%20%2F%2F%20One%20by%20one%20extract%20an%20element%20from%20heap%0A%20%20%20%20for%20(int%20i%3Dn-1%3B%20i%3E%3D0%3B%20i–)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20Move%20current%20root%20to%20end%0A%20%20%20%20%20%20%20%20swap(arr%5B0%5D%2C%20arr%5Bi%5D)%3B%0A%20%0A%20%20%20%20%20%20%20%20%2F%2F%20call%20max%20heapify%20on%20the%20reduced%20heap%0A%20%20%20%20%20%20%20%20heapify(arr%2C%20i%2C%200)%3B%0A%20%20%20%20%7D%0A%7D%0A%20%0A%2F*%20A%20utility%20function%20to%20print%20array%20of%20size%20n%20*%2F%0Avoid%20printArray(int%20arr%5B%5D%2C%20int%20n)%0A%7B%0A%20%20%20%20for%20(int%20i%3D0%3B%20i%3Cn%3B%20%2B%2Bi)%0A%20%20%20%20%20%20%20%20cout%20%3C%3C%20arr%5Bi%5D%20%3C%3C%20%22%20%22%3B%0A%20%20%20%20cout%20%3C%3C%20%22%5Cn%22%3B%0A%7D%0A%20%0A%2F%2F%20Driver%20program%0Aint%20main()%0A%7B%0A%20%20%20%20int%20arr%5B%5D%20%3D%20%7B12%2C%2011%2C%2013%2C%205%2C%206%2C%207%7D%3B%0A%20%20%20%20int%20n%20%3D%20sizeof(arr)%2Fsizeof(arr%5B0%5D)%3B%0A%20%0A%20%20%20%20heapSort(arr%2C%20n)%3B%0A%20%0A%20%20%20%20cout%20%3C%3C%20%22Sorted%20array%20is%20%5Cn%22%3B%0A%20%20%20%20printArray(arr%2C%20n)%3B%0A%7D” message=”” highlight=”” provider=”manual”/]Output:
Sorted array is 5 6 7 11 12 13