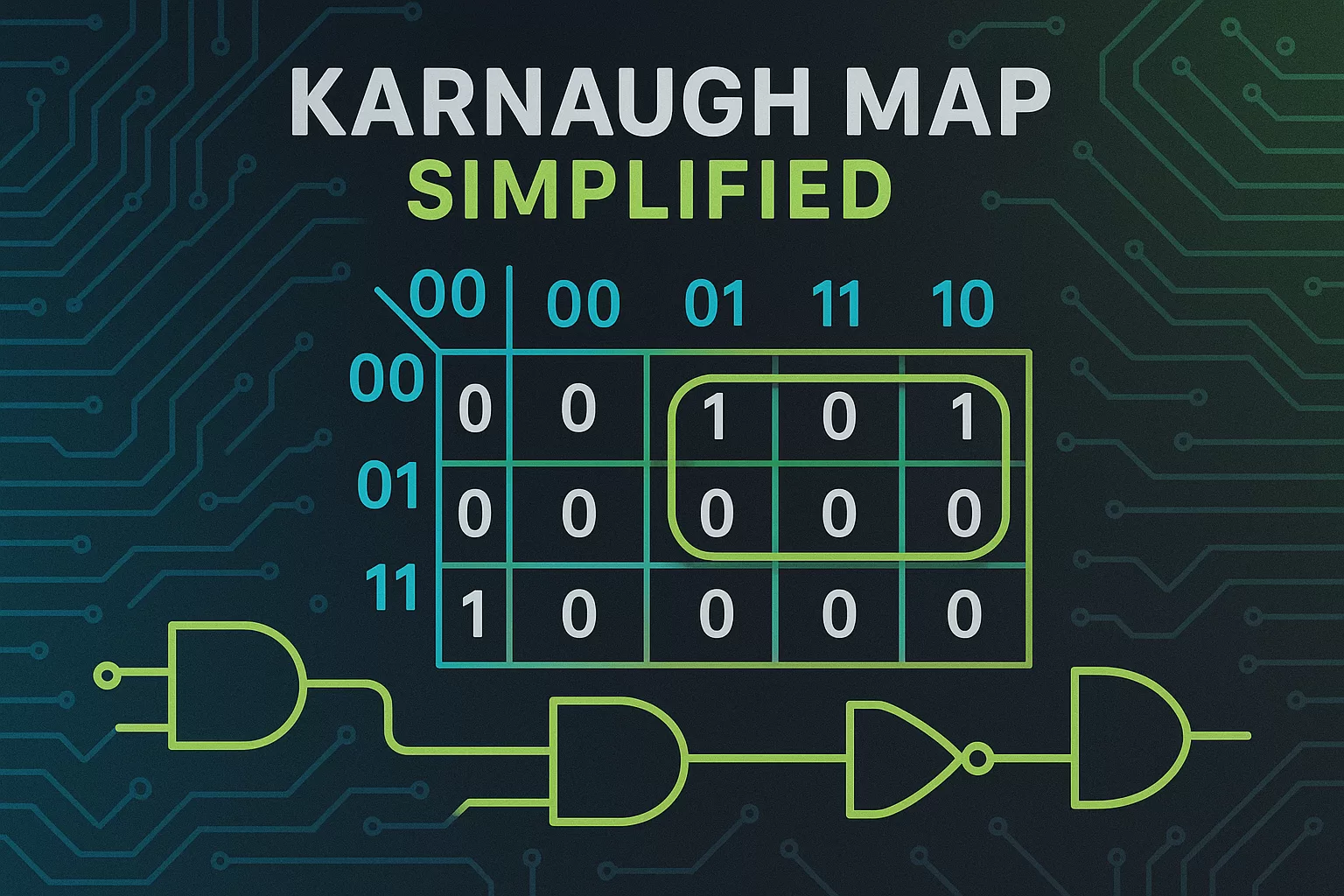
In digital electronics, simplifying Boolean expressions is crucial for designing efficient logic circuits. One of the most widely used techniques to achieve this is the Karnaugh Map, also known as the K Map. Whether you’re a student or a budding engineer, understanding how to solve Boolean functions using K-Map can save time and reduce complexity in your designs.
In this guide, you’ll learn:
- What a Karnaugh Map is
- Why K-Maps are important in digital logic
- How to solve and reduce Boolean expressions using a 4-variable map
- Real examples with step-by-step solutions
Let’s dive in.
🧠 What Is Karnaugh Map (K-Map)?
A Karnaugh Map (K-map) is a graphical method for simplifying Boolean expressions. It was developed by Maurice Karnaugh in 1953 and is used to visualize and eliminate redundant logic in Boolean algebra.
Instead of manually solving Boolean expressions using algebraic identities, it provide a faster and error-free method by organizing truth table outputs into a 2D grid.
🔍 What is K Maps Uses?
K Maps help:
- Minimize Boolean expressions
- Reduce the number of logic gates needed
- Create efficient digital circuits
- Detect redundant terms
The result? You get optimized logic expressions that are easier to implement using hardware like AND, OR, and NOT gates.
🧾 What is K-Map Structure
The structure depends on the number of variables:
| Variables | Grid Size | Example |
|---|---|---|
| 2 | 2×2 | A, B |
| 3 | 2×4 | A, B, C |
| 4 | 4×4 | A, B, C, D |
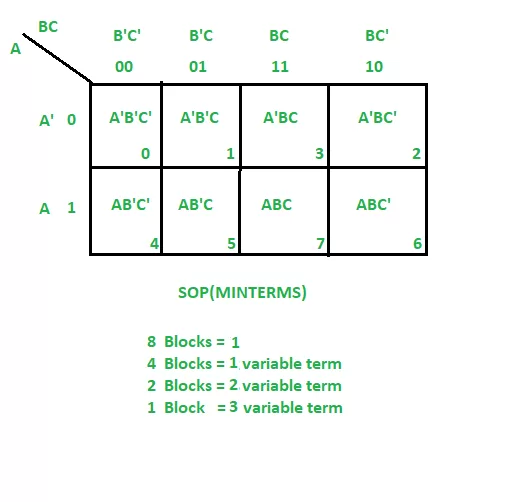
Each cell in a Karnaugh Map corresponds to a minterm, representing a unique binary combination of inputs. The order of cells follows Gray code, ensuring that adjacent cells differ by only one variable.
🧪 What Is a 4 Variable Karnaugh Map?
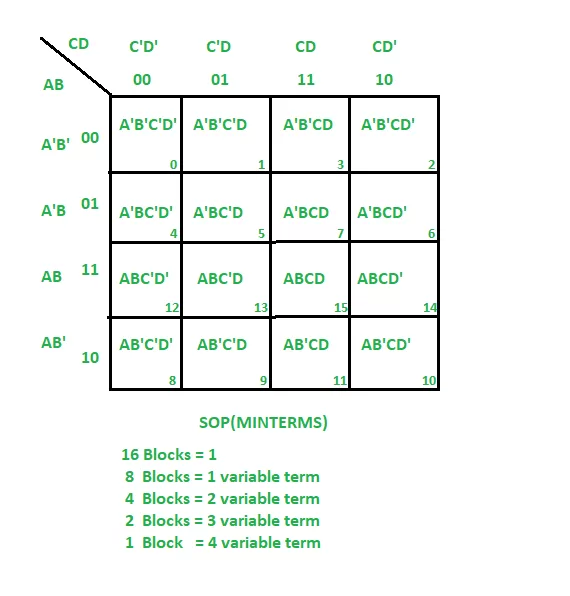
A 4 variable Karnaugh map is one of the most common types used in practice. It includes 16 cells arranged in a 4×4 grid. Each cell represents one of the 16 minterms from the truth table of four input variables: A, B, C, and D.
The cell positions follow this layout:
luaCopyEdit CD
00 01 11 10
+----------------
AB |
00 | m0 m1 m3 m2
01 | m4 m5 m7 m6
11 | m12 m13 m15 m14
10 | m8 m9 m11 m10
Note how the column and row labels are in Gray code (00, 01, 11, 10), not binary order.
Steps to Solve Expression using K-map
- Select the K-map according to the number of variables.
- Identify minterms or maxterms as given in the problem.
- For SOP put 1’s in blocks of K-map respective to the minterms (0’s elsewhere).
- For POS put 0’s in blocks of K-map respective to the max terms (1’s elsewhere).
- Make rectangular groups containing total terms in power of two like 2,4,8 ..(except 1) and try to cover as many elements as you can in one group.
- From the groups made in step 5 find the product terms and sum them up for SOP form.
SOP FORM(Sum of Product Form)
SOP form is way to simplify and write Boolean expressions using AND to combine inputs and OP to combine the results.
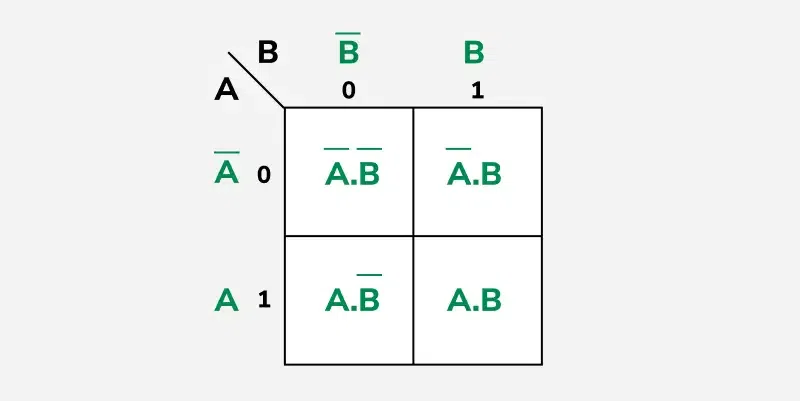
1. K-map for 2 variables
In the 2 variable k-map, four squares are constructed. Each square contains one term of expression with two variables.
2. K-map of 3 variables
Z= ΣA,B,C(1,3,6,7)
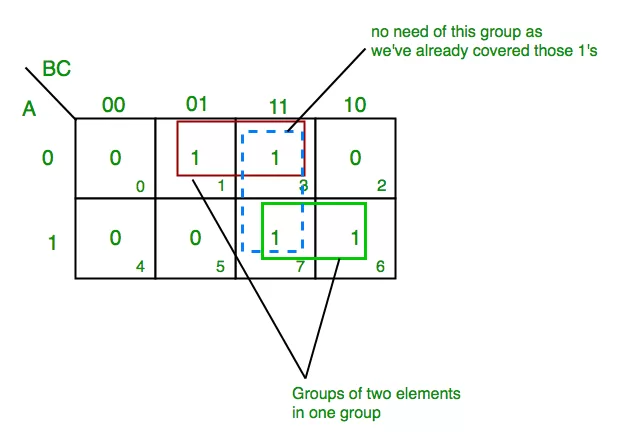
From red group we get product term:
A’C
From green group we get product term:
AB
Summing these product terms we get- Final expression (A’C+AB)
3. K-map for 4 variables
F(A,B,C,D)=Σ(0,2,5,7,8,10,13,15)

From red group we get product term:
AB
From green group we get product term:
A'B'
Summing these product terms we get- Final expression (AB+A’B’).
POS FORM (Product of Sum Form)
POS form is a way to simplify and write Boolean expressions using OR to combine terms inside parentheses and then AND to combine those groups.
1.K-map of 2 variables
In the 2 variable k-map, four squares are constructed. Each square contains one term of expression with two variables.

2. K-map of 3 variables
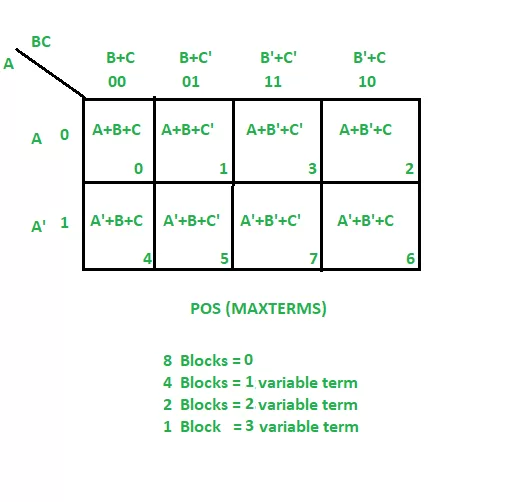
F(A,B,C)=Σ(0,3,6,7)
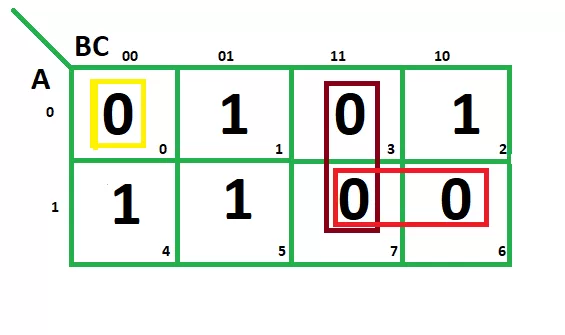
From red group we find terms
A B
Taking complement of these two
A' B'
Now sum up them
(A' + B')
From brown group we find terms
B C
Taking complement of these two terms
B’ C’
Now sum up them
(B’+C’)
From yellow group we find terms
A' B' C’
Taking complement of these two
A B C
Now sum up them
(A + B + C)
We will take product of these three terms : Final expression –
(A' + B’) (B’ + C’) (A + B + C)
3. K-map of 4 variables
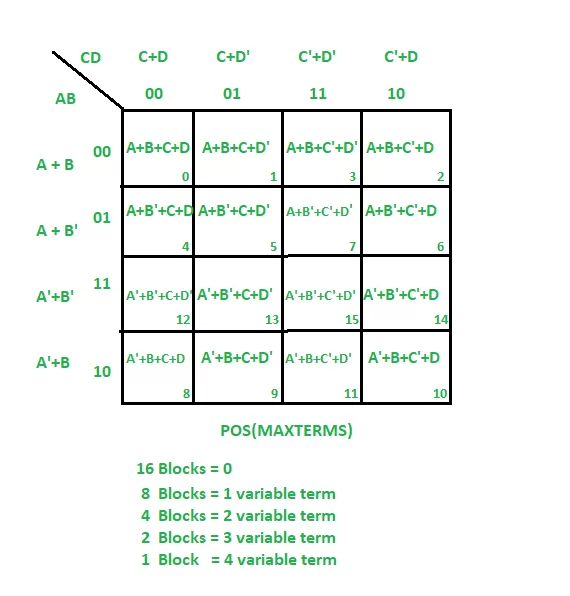
F(A,B,C,D)=Σ(3,5,7,8,10,11,12,13)
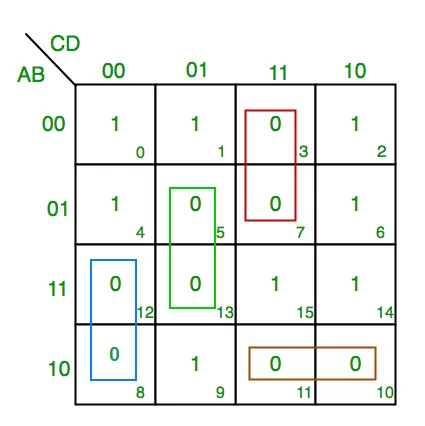
From green group we find terms
C’ D B
Taking their complement and summing them
(C+D’+B’)
From red group we find terms
C D A’
Taking their complement and summing them
(C’+D’+A)
From blue group we find terms
A C’ D’
Taking their complement and summing them
(A’+C+D)
From brown group we find terms
A B’ C
Taking their complement and summing them
(A’+B+C’)
Finally we express these as product –
(C+D’+B’).(C’+D’+A).(A’+C+D).(A’+B+C’)
Advantages of
- Makes Logic Simpler: It makes complicated Boolean expressions simpler.
- Minimizes Logic Gates: Simplifying the logic helps us to use fewer logic gates, making circuits more efficient.
- Reduce Errors: The visual representation helps to avoid errors while simplifying.
- Time-Saving: It’s quicker than traditional methods for simplifying logic.
- No need for Boolean Laws: It doesn’t require deep knowledge of Boolean laws, making it easy for beginners.
Disadvantages of
- Limited to Fewer Variables: are best suited for 2 to 4 variables and above it, process becomes hard and complicated to manage.
- Not suitable for all functions: In some cases, its hard to group terms correctly, leading to errors and making simplification difficult.
- Space Limitations: As the number of variables increases, the grid becomes too large to handle easily.
- Requires Careful Grouping: Sometimes incorrect grouping of terms can cause mistakes in logic simplification.
✅ Example 1: Solve Using K-Map
Given Boolean function:f(a, b, c, d) = m(1, 3, 4, 5, 6, 7, 9, 11, 12, 13, 14, 15)
Step 1: Plot the minterms
Mark 1 in the cells corresponding to the minterms listed.
Step 2: Group adjacent 1s
- Group of 8: Covers minterms 12, 13, 14, 15, 4, 5, 6, 7
- Group of 4: Covers minterms 1, 3, 9, 11
Step 3: Write simplified expression
- First group (8-cell group) = B
- Second group (4-cell group) = A’D
Final Answer:f = B + A'D
This is the simplified Boolean expression using K-map.
✅ Example 2: Reduce Using K-Map
Given Boolean Function:f(a, b, c, d) = ∑(1, 3, 5, 7, 9, 11, 12,13,14,15)
Let’s reduce this using a 4-variable Karnaugh Map.
Step 1: Fill It
Plot 1s in the following cells: 1, 3, 5, 7, 9, 11, 12, 13, 14, 15
Step 2: Group cells into 2ⁿ blocks
- Group of 8: Minterms 12–15 and 5, 7, 13, 14
- Group of 4: Minterms 1, 3, 9, 11
Step 3: Simplify
- First group = B
- Second group = A’D
Simplified Expression:f = B + A'D (Same result as the previous example)
This shows how multiple Boolean functions can reduce to the same minimal form using K-maps.
💡 Tips for Solving K-Map Problems
- Always follow Gray code order (00, 01, 11, 10)
- Group sizes must be powers of two: 1, 2, 4, 8
- Larger groups = better simplification
- You can wrap around edges of the map (treat K-map as a torus)
- Minimize overlapping groups to avoid unnecessary repetition
📌 When to Use SOP and POS ?
- SOP (Sum of Products): Use when the function is defined using minterms (1s)
- POS (Product of Sums): Use when the function is defined using maxterms (0s)
🧩 Common Applications
- Logic gate minimization
- Simplifying control logic in embedded systems
- Reducing programmable logic arrays (PLAs)
- Designing combinational circuits like multiplexers, decoders, etc.
❓ FAQ: Karnaugh Map (K-Map)
1. What is K Map used for?
It simplifies Boolean expressions by visually grouping terms. It helps reduce logic gate count in digital circuits.
2. What is the difference between K-Map and Boolean algebra?
While Boolean algebra uses rules and identities, a It offers a visual, faster, and more intuitive method to simplify logic.
3. What is a 4-variable Karnaugh Map?
It is a 4×4 grid used to simplify expressions with four inputs (A, B, C, D). Each cell corresponds to a minterm from the function’s truth table.
4. How do I solve using K-map?
Plot the given minterms, group adjacent 1s in powers of 2 (1, 2, 4, 8), and extract the simplified expression from the groups.
5. What is the minimized expression of f(a,b,c,d) = ∑(1,3,5,7,9,11,12,13,14,15)?
The simplified expression is:
f = B + A’D
🔚 Final Thoughts
Mastering the Karnaugh Map (K-map) is essential for anyone working with digital logic. It not only reduces Boolean expressions quickly but also helps you design efficient and cost-effective logic circuits.
By practicing with examples like the ones above, you’ll become confident in solving even complex 4-variable K-Map problems and minimizing Boolean functions with ease.
🚀 Looking to take your skills further?
Check out Embedded System Internship programs and turn theory into practice. Work on real-time microcontroller projects, learn sensor integration, and build systems that respond to the real world.
📚 Related Reads
- 🔗 The Top 8 Logic Gates Essential for IT Career – Learn how fundamental logic gates power everything from digital circuits to microprocessors.
- 🔗 Binary Arithmetic Explained with Examples – Dive into binary math operations with clear examples every beginner can understand.