A triangulation of a convex polygon is formed by drawing diagonals between non-adjacent vertices (corners) such that the diagonals never intersect. The problem is to find the cost of triangulation with the minimum cost. The cost of a triangulation is sum of the weights of its component triangles. Weight of each triangle is its perimeter (sum of lengths of all sides)
See following example taken from this source.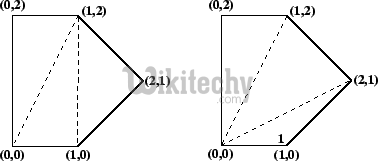
Two triangulations of the same convex pentagon. The triangulation on the left has a cost of 8 + 2√2 + 2√5 (approximately 15.30), the one on the right has a cost of 4 + 2√2 + 4√5 (approximately 15.77).
This problem has recursive substructure. The idea is to divide the polygon into three parts: a single triangle, the sub-polygon to the left, and the sub-polygon to the right. We try all possible divisions like this and find the one that minimizes the cost of the triangle plus the cost of the triangulation of the two sub-polygons.
Let Minimum Cost of triangulation of vertices from i to j be minCost(i, j)
If j <= i + 2 Then
minCost(i, j) = 0
Else
minCost(i, j) = Min { minCost(i, k) + minCost(k, j) + cost(i, k, j) }
Here k varies from 'i+1' to 'j-1'
Cost of a triangle formed by edges (i, j), (j, k) and (k, j) is
cost(i, j, k) = dist(i, j) + dist(j, k) + dist(k, j)
[ad type=”banner”]
Following is C++ implementation of above naive recursive formula.
[pastacode lang=”cpp” manual=”%2F%2F%20Recursive%20implementation%20for%20minimum%20cost%20convex%20polygon%20triangulation%0A%23include%20%3Ciostream%3E%0A%23include%20%3Ccmath%3E%0A%23define%20MAX%201000000.0%0Ausing%20namespace%20std%3B%0A%20%0A%2F%2F%20Structure%20of%20a%20point%20in%202D%20plane%0Astruct%20Point%0A%7B%0A%20%20%20%20int%20x%2C%20y%3B%0A%7D%3B%0A%20%0A%2F%2F%20Utility%20function%20to%20find%20minimum%20of%20two%20double%20values%0Adouble%20min(double%20x%2C%20double%20y)%0A%7B%0A%20%20%20%20return%20(x%20%3C%3D%20y)%3F%20x%20%3A%20y%3B%0A%7D%0A%20%0A%2F%2F%20A%20utility%20function%20to%20find%20distance%20between%20two%20points%20in%20a%20plane%0Adouble%20dist(Point%20p1%2C%20Point%20p2)%0A%7B%0A%20%20%20%20return%20sqrt((p1.x%20-%20p2.x)*(p1.x%20-%20p2.x)%20%2B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20(p1.y%20-%20p2.y)*(p1.y%20-%20p2.y))%3B%0A%7D%0A%20%0A%2F%2F%20A%20utility%20function%20to%20find%20cost%20of%20a%20triangle.%20The%20cost%20is%20considered%0A%2F%2F%20as%20perimeter%20(sum%20of%20lengths%20of%20all%20edges)%20of%20the%20triangle%0Adouble%20cost(Point%20points%5B%5D%2C%20int%20i%2C%20int%20j%2C%20int%20k)%0A%7B%0A%20%20%20%20Point%20p1%20%3D%20points%5Bi%5D%2C%20p2%20%3D%20points%5Bj%5D%2C%20p3%20%3D%20points%5Bk%5D%3B%0A%20%20%20%20return%20dist(p1%2C%20p2)%20%2B%20dist(p2%2C%20p3)%20%2B%20dist(p3%2C%20p1)%3B%0A%7D%0A%20%0A%2F%2F%20A%20recursive%20function%20to%20find%20minimum%20cost%20of%20polygon%20triangulation%0A%2F%2F%20The%20polygon%20is%20represented%20by%20points%5Bi..j%5D.%0Adouble%20mTC(Point%20points%5B%5D%2C%20int%20i%2C%20int%20j)%0A%7B%0A%20%20%20%2F%2F%20There%20must%20be%20at%20least%20three%20points%20between%20i%20and%20j%0A%20%20%20%2F%2F%20(including%20i%20and%20j)%0A%20%20%20if%20(j%20%3C%20i%2B2)%0A%20%20%20%20%20%20return%200%3B%0A%20%0A%20%20%20%2F%2F%20Initialize%20result%20as%20infinite%0A%20%20%20double%20res%20%3D%20MAX%3B%0A%20%0A%20%20%20%2F%2F%20Find%20minimum%20triangulation%20by%20considering%20all%0A%20%20%20for%20(int%20k%3Di%2B1%3B%20k%3Cj%3B%20k%2B%2B)%0A%20%20%20%20%20%20%20%20res%20%3D%20min(res%2C%20(mTC(points%2C%20i%2C%20k)%20%2B%20mTC(points%2C%20k%2C%20j)%20%2B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20cost(points%2C%20i%2C%20k%2C%20j)))%3B%0A%20%20%20return%20%20res%3B%0A%7D%0A%20%0A%2F%2F%20Driver%20program%20to%20test%20above%20functions%0Aint%20main()%0A%7B%0A%20%20%20%20Point%20points%5B%5D%20%3D%20%7B%7B0%2C%200%7D%2C%20%7B1%2C%200%7D%2C%20%7B2%2C%201%7D%2C%20%7B1%2C%202%7D%2C%20%7B0%2C%202%7D%7D%3B%0A%20%20%20%20int%20n%20%3D%20sizeof(points)%2Fsizeof(points%5B0%5D)%3B%0A%20%20%20%20cout%20%3C%3C%20mTC(points%2C%200%2C%20n-1)%3B%0A%20%20%20%20return%200%3B%0A%7D” message=”C++” highlight=”” provider=”manual”/]Output:
15.3006
The above problem is similar to Matrix Chain Multiplication. The following is recursion tree for mTC(points[], 0, 4).
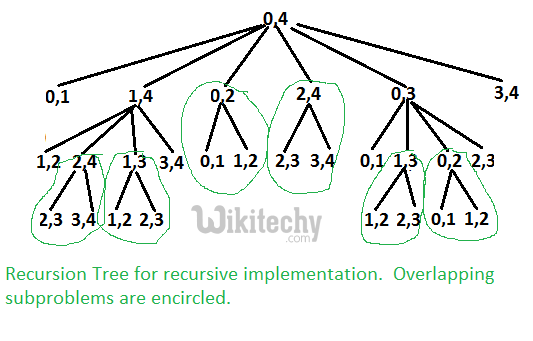
It can be easily seen in the above recursion tree that the problem has many overlapping subproblems. Since the problem has both properties: Optimal Substructure and Overlapping Subproblems, it can be efficiently solved using dynamic programming.
[ad type=”banner”]Following is C++ implementation of dynamic programming solution.
[pastacode lang=”cpp” manual=”%2F%2F%20A%20Dynamic%20Programming%20based%20program%20to%20find%20minimum%20cost%20of%20convex%0A%2F%2F%20polygon%20triangulation%0A%23include%20%3Ciostream%3E%0A%23include%20%3Ccmath%3E%0A%23define%20MAX%201000000.0%0Ausing%20namespace%20std%3B%0A%20%0A%2F%2F%20Structure%20of%20a%20point%20in%202D%20plane%0Astruct%20Point%0A%7B%0A%20%20%20%20int%20x%2C%20y%3B%0A%7D%3B%0A%20%0A%2F%2F%20Utility%20function%20to%20find%20minimum%20of%20two%20double%20values%0Adouble%20min(double%20x%2C%20double%20y)%0A%7B%0A%20%20%20%20return%20(x%20%3C%3D%20y)%3F%20x%20%3A%20y%3B%0A%7D%0A%20%0A%2F%2F%20A%20utility%20function%20to%20find%20distance%20between%20two%20points%20in%20a%20plane%0Adouble%20dist(Point%20p1%2C%20Point%20p2)%0A%7B%0A%20%20%20%20return%20sqrt((p1.x%20-%20p2.x)*(p1.x%20-%20p2.x)%20%2B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20(p1.y%20-%20p2.y)*(p1.y%20-%20p2.y))%3B%0A%7D%0A%20%0A%2F%2F%20A%20utility%20function%20to%20find%20cost%20of%20a%20triangle.%20The%20cost%20is%20considered%0A%2F%2F%20as%20perimeter%20(sum%20of%20lengths%20of%20all%20edges)%20of%20the%20triangle%0Adouble%20cost(Point%20points%5B%5D%2C%20int%20i%2C%20int%20j%2C%20int%20k)%0A%7B%0A%20%20%20%20Point%20p1%20%3D%20points%5Bi%5D%2C%20p2%20%3D%20points%5Bj%5D%2C%20p3%20%3D%20points%5Bk%5D%3B%0A%20%20%20%20return%20dist(p1%2C%20p2)%20%2B%20dist(p2%2C%20p3)%20%2B%20dist(p3%2C%20p1)%3B%0A%7D%0A%20%0A%2F%2F%20A%20Dynamic%20programming%20based%20function%20to%20find%20minimum%20cost%20for%20convex%0A%2F%2F%20polygon%20triangulation.%0Adouble%20mTCDP(Point%20points%5B%5D%2C%20int%20n)%0A%7B%0A%20%20%20%2F%2F%20There%20must%20be%20at%20least%203%20points%20to%20form%20a%20triangle%0A%20%20%20if%20(n%20%3C%203)%0A%20%20%20%20%20%20return%200%3B%0A%20%0A%20%20%20%2F%2F%20table%20to%20store%20results%20of%20subproblems.%20%20table%5Bi%5D%5Bj%5D%20stores%20cost%20of%0A%20%20%20%2F%2F%20triangulation%20of%20points%20from%20i%20to%20j.%20%20The%20entry%20table%5B0%5D%5Bn-1%5D%20stores%0A%20%20%20%2F%2F%20the%20final%20result.%0A%20%20%20double%20table%5Bn%5D%5Bn%5D%3B%0A%20%0A%20%20%20%2F%2F%20Fill%20table%20using%20above%20recursive%20formula.%20Note%20that%20the%20table%0A%20%20%20%2F%2F%20is%20filled%20in%20diagonal%20fashion%20i.e.%2C%20from%20diagonal%20elements%20to%0A%20%20%20%2F%2F%20table%5B0%5D%5Bn-1%5D%20which%20is%20the%20result.%0A%20%20%20for%20(int%20gap%20%3D%200%3B%20gap%20%3C%20n%3B%20gap%2B%2B)%0A%20%20%20%7B%0A%20%20%20%20%20%20for%20(int%20i%20%3D%200%2C%20j%20%3D%20gap%3B%20j%20%3C%20n%3B%20i%2B%2B%2C%20j%2B%2B)%0A%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20if%20(j%20%3C%20i%2B2)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20table%5Bi%5D%5Bj%5D%20%3D%200.0%3B%0A%20%20%20%20%20%20%20%20%20%20else%0A%20%20%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20table%5Bi%5D%5Bj%5D%20%3D%20MAX%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20for%20(int%20k%20%3D%20i%2B1%3B%20k%20%3C%20j%3B%20k%2B%2B)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20double%20val%20%3D%20table%5Bi%5D%5Bk%5D%20%2B%20table%5Bk%5D%5Bj%5D%20%2B%20cost(points%2Ci%2Cj%2Ck)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(table%5Bi%5D%5Bj%5D%20%3E%20val)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20table%5Bi%5D%5Bj%5D%20%3D%20val%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%7D%0A%20%20%20%7D%0A%20%20%20return%20%20table%5B0%5D%5Bn-1%5D%3B%0A%7D%0A%20%0A%2F%2F%20Driver%20program%20to%20test%20above%20functions%0Aint%20main()%0A%7B%0A%20%20%20%20Point%20points%5B%5D%20%3D%20%7B%7B0%2C%200%7D%2C%20%7B1%2C%200%7D%2C%20%7B2%2C%201%7D%2C%20%7B1%2C%202%7D%2C%20%7B0%2C%202%7D%7D%3B%0A%20%20%20%20int%20n%20%3D%20sizeof(points)%2Fsizeof(points%5B0%5D)%3B%0A%20%20%20%20cout%20%3C%3C%20mTCDP(points%2C%20n)%3B%0A%20%20%20%20return%200%3B%0A%7D” message=”C++” highlight=”” provider=”manual”/]Output:
15.3006
Time complexity of the above dynamic programming solution is O(n3).
[ad type=”banner”]