Implementation Dequeue Using Circular Array:
Dequeue or Double Ended Queue is a generalized version of Queue data structure that allows insert and delete at both ends.In previous post we had discussed introduction of dequeue. Now in this post we see how we implement dequeue Using circular array.
Operations on Dequeue:
Mainly the following four basic operations are performed on queue:
insertFront(): Adds an item at the front of Dequeue.
insertRear(): Adds an item at the rear of Dequeue.
deleteFront(): Deletes an item from front of Dequeue.
deleteRear(): Deletes an item from rear of Dequeue.
In addition to above operations, following operations are also supported
getFront(): Gets the front item from queue.
getRear(): Gets the last item from queue.
isEmpty(): Checks whether Dequeue is empty or not.
isFull(): Checks whether Dequeue is full or not.
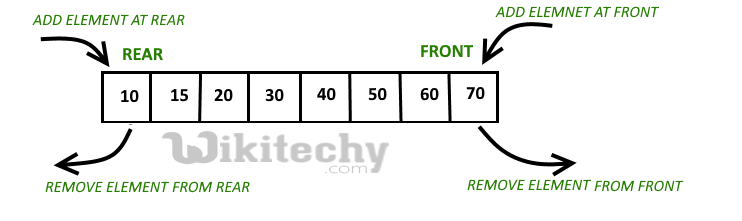
Circular array implementation dequeue
For implementing dequeue, we need to keep track of two indices, front and rear. We enqueue(push) an item at the rear or the front end of queue and dequeue(pop) an item from both rear and front end.
Working
1. Create an empty array ‘arr’ of size ‘n’
initialize front = -1 , rear = 0
Inserting First element in dequeue either front end or read end they both lead to the same result.
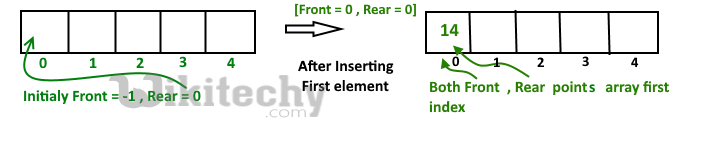
after insert Front Points = 0 and Rear points = 0
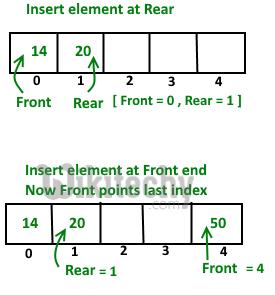
Insert Elements at Rear end
a). First we check dequeue if Full or Not
b). IF Rear == Size-1
then reinitialize Rear = 0 ;
Else increment Rear by '1'
and push current key into Arr[ rear ] = key
Front remain same.
[ad type=”banner”]
Insert Elements at Front end
a). First we check dequeue if Full or Not
b). IF Front == 0 || initial position, move Front
to points last index of array
front = size - 1
Else decremented front by '1' and push
current key into Arr[ Front] = key
Rear remain same.
Delete Element From Rear end
a). first Check dequeue is Empty or Not
b). If dequeue has only one element
front = -1 ; rear =-1 ;
Else IF Rear points to the first index of array
it's means we have to move rear to points
last index [ now first inserted element at
front end become rear end ]
rear = size-1 ;
Else || decrease rear by '1'
rear = rear-1;
[ad type=”banner”]
Delete Element From Front end
a). first Check dequeue is Empty or Not
b). If dequeue has only one element
front = -1 ; rear =-1 ;
Else IF front points to the last index of the array
it's means we have no more elements in array so
we move front to points first index of array
front = 0 ;
Else || increment Front by '1'
front = front+1;
Java Implementation Dequeue Using Circular Array:
[pastacode lang=”java” manual=”%2F%2F%20Java%20implementation%20of%20De-queue%20using%20circular%0A%2F%2F%20array%0A%20%20%0A%2F%2F%20A%20structure%20to%20represent%20a%20Deque%0Aclass%20Deque%0A%7B%0A%20%20%20%20static%20final%20int%20MAX%20%3D%20100%3B%0A%20%20%20%20int%20%20arr%5B%5D%3B%0A%20%20%20%20int%20%20front%3B%0A%20%20%20%20int%20%20rear%3B%0A%20%20%20%20int%20%20size%3B%0A%20%20%20%20%20%0A%20%20%20%20public%20Deque(int%20size)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20arr%20%3D%20new%20int%5BMAX%5D%3B%0A%20%20%20%20%20%20%20%20front%20%3D%20-1%3B%0A%20%20%20%20%20%20%20%20rear%20%3D%200%3B%0A%20%20%20%20%20%20%20%20this.size%20%3D%20size%3B%0A%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%2F*%2F%2F%20Operations%20on%20Deque%3A%0A%20%20%20%20void%20%20insertfront(int%20key)%3B%0A%20%20%20%20void%20%20insertrear(int%20key)%3B%0A%20%20%20%20void%20%20deletefront()%3B%0A%20%20%20%20void%20%20deleterear()%3B%0A%20%20%20%20bool%20%20isFull()%3B%0A%20%20%20%20bool%20%20isEmpty()%3B%0A%20%20%20%20int%20%20getFront()%3B%0A%20%20%20%20int%20%20getRear()%3B*%2F%0A%20%20%0A%20%20%20%20%2F%2F%20Checks%20whether%20Deque%20is%20full%20or%20not.%0A%20%20%20%20boolean%20isFull()%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20return%20((front%20%3D%3D%200%20%26%26%20rear%20%3D%3D%20size-1)%7C%7C%0A%20%20%20%20%20%20%20%20%20%20%20%20front%20%3D%3D%20rear%2B1)%3B%0A%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%2F%2F%20Checks%20whether%20Deque%20is%20empty%20or%20not.%0A%20%20%20%20boolean%20isEmpty%20()%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20return%20(front%20%3D%3D%20-1)%3B%0A%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%2F%2F%20Inserts%20an%20element%20at%20front%0A%20%20%20%20void%20insertfront(int%20key)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20check%20whether%20Deque%20if%20%20full%20or%20not%0A%20%20%20%20%20%20%20%20if%20(isFull())%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20System.out.println(%22Overflow%22)%3B%20%0A%20%20%20%20%20%20%20%20%20%20%20%20return%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%20%20%20%20%2F%2F%20If%20queue%20is%20initially%20empty%0A%20%20%20%20%20%20%20%20if%20(front%20%3D%3D%20-1)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20front%20%3D%200%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20rear%20%3D%200%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%2F%2F%20front%20is%20at%20first%20position%20of%20queue%0A%20%20%20%20%20%20%20%20else%20if%20(front%20%3D%3D%200)%0A%20%20%20%20%20%20%20%20%20%20%20%20front%20%3D%20size%20-%201%20%3B%0A%20%20%0A%20%20%20%20%20%20%20%20else%20%2F%2F%20decrement%20front%20end%20by%20’1’%0A%20%20%20%20%20%20%20%20%20%20%20%20front%20%3D%20front-1%3B%0A%20%20%0A%20%20%20%20%20%20%20%20%2F%2F%20insert%20current%20element%20into%20Deque%0A%20%20%20%20%20%20%20%20arr%5Bfront%5D%20%3D%20key%20%3B%0A%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%2F%2F%20function%20to%20inset%20element%20at%20rear%20end%0A%20%20%20%20%2F%2F%20of%20Deque.%0A%20%20%20%20void%20insertrear(int%20key)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20if%20(isFull())%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20System.out.println(%22%20Overflow%20%22)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20return%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%20%20%20%20%2F%2F%20If%20queue%20is%20initially%20empty%0A%20%20%20%20%20%20%20%20if%20(front%20%3D%3D%20-1)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20front%20%3D%200%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20rear%20%3D%200%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%20%20%20%20%2F%2F%20rear%20is%20at%20last%20position%20of%20queue%0A%20%20%20%20%20%20%20%20else%20if%20(rear%20%3D%3D%20size-1)%0A%20%20%20%20%20%20%20%20%20%20%20%20rear%20%3D%200%3B%0A%20%20%0A%20%20%20%20%20%20%20%20%2F%2F%20increment%20rear%20end%20by%20’1’%0A%20%20%20%20%20%20%20%20else%0A%20%20%20%20%20%20%20%20%20%20%20%20rear%20%3D%20rear%2B1%3B%0A%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%2F%2F%20insert%20current%20element%20into%20Deque%0A%20%20%20%20%20%20%20%20arr%5Brear%5D%20%3D%20key%20%3B%0A%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%2F%2F%20Deletes%20element%20at%20front%20end%20of%20Deque%0A%20%20%20%20void%20deletefront()%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20check%20whether%20Deque%20is%20empty%20or%20not%0A%20%20%20%20%20%20%20%20if%20(isEmpty())%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20System.out.println(%22Queue%20Underflow%5Cn%22)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%20%20%20%20%2F%2F%20Deque%20has%20only%20one%20element%0A%20%20%20%20%20%20%20%20if%20(front%20%3D%3D%20rear)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20front%20%3D%20-1%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20rear%20%3D%20-1%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20else%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20back%20to%20initial%20position%0A%20%20%20%20%20%20%20%20%20%20%20%20if%20(front%20%3D%3D%20size%20-1)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20front%20%3D%200%3B%0A%20%20%0A%20%20%20%20%20%20%20%20%20%20%20%20else%20%2F%2F%20increment%20front%20by%20’1’%20to%20remove%20current%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20front%20value%20from%20Deque%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20front%20%3D%20front%2B1%3B%0A%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%2F%2F%20Delete%20element%20at%20rear%20end%20of%20Deque%0A%20%20%20%20void%20deleterear()%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20if%20(isEmpty())%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20System.out.println(%22%20Underflow%22)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%20%20%20%20%2F%2F%20Deque%20has%20only%20one%20element%0A%20%20%20%20%20%20%20%20if%20(front%20%3D%3D%20rear)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20front%20%3D%20-1%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20rear%20%3D%20-1%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20else%20if%20(rear%20%3D%3D%200)%0A%20%20%20%20%20%20%20%20%20%20%20%20rear%20%3D%20size-1%3B%0A%20%20%20%20%20%20%20%20else%0A%20%20%20%20%20%20%20%20%20%20%20%20rear%20%3D%20rear-1%3B%0A%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%2F%2F%20Returns%20front%20element%20of%20Deque%0A%20%20%20%20int%20getFront()%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20check%20whether%20Deque%20is%20empty%20or%20not%0A%20%20%20%20%20%20%20%20if%20(isEmpty())%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20System.out.println(%22%20Underflow%22)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20-1%20%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20return%20arr%5Bfront%5D%3B%0A%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%2F%2F%20function%20return%20rear%20element%20of%20Deque%0A%20%20%20%20int%20getRear()%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20check%20whether%20Deque%20is%20empty%20or%20not%0A%20%20%20%20%20%20%20%20if(isEmpty()%20%7C%7C%20rear%20%3C%200)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20System.out.println(%22%20Underflow%5Cn%22)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20-1%20%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20return%20arr%5Brear%5D%3B%0A%20%20%20%20%7D%0A%20%20%0A%20%20%20%20%2F%2F%20Driver%20program%20to%20test%20above%20function%0A%20%20%20%20public%20static%20void%20main(String%5B%5D%20args)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20Deque%20dq%20%3D%20new%20Deque(5)%3B%0A%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20System.out.println(%22Insert%20element%20at%20rear%20end%20%20%3A%205%20%22)%3B%0A%20%20%20%20%20%20%20%20%20dq.insertrear(5)%3B%0A%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20System.out.println(%22insert%20element%20at%20rear%20end%20%3A%2010%20%22)%3B%0A%20%20%20%20%20%20%20%20%20dq.insertrear(10)%3B%0A%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20System.out.println(%22get%20rear%20element%20%3A%20%22%2B%20dq.getRear())%3B%0A%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20dq.deleterear()%3B%0A%20%20%20%20%20%20%20%20%20System.out.println(%22After%20delete%20rear%20element%20new%20rear%20become%20%3A%20%22%20%2B%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20dq.getRear())%3B%0A%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20System.out.println(%22inserting%20element%20at%20front%20end%22)%3B%0A%20%20%20%20%20%20%20%20%20dq.insertfront(15)%3B%0A%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20System.out.println(%22get%20front%20element%3A%20%22%20%2Bdq.getFront())%3B%0A%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20dq.deletefront()%3B%0A%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20System.out.println(%22After%20delete%20front%20element%20new%20front%20become%20%3A%20%22%20%2B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%2B%20%20dq.getFront())%3B%0A%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%7D%0A%7D%0A” message=”” highlight=”” provider=”manual”/]Output:
insert element at rear end : 5 insert element at rear end : 10 get rear element : 10 After delete rear element new rear become : 5 inserting element at front end get front element : 15 After delete front element new front become : 5
Time Complexity: Time complexity of all operations like insertfront(), insertlast(), deletefront(), deletelast() is O(1).
[ad type=”banner”]