Largest Sum Contiguous Subarray
Write an efficient Python program to find the sum of contiguous subarray within a one-dimensional array of numbers which has the largest sum.
Kadane’s Algorithm:
Initialize:
max_so_far = 0
max_ending_here = 0
Loop for each element of the array
(a) max_ending_here = max_ending_here + a[i]
(b) if(max_ending_here < 0)
max_ending_here = 0
(c) if(max_so_far < max_ending_here)
max_so_far = max_ending_here
return max_so_far
[ad type=”banner”]
Explanation:
Simple idea of the Kadane’s algorithm is to look for all positive contiguous segments of the array (max_ending_here is used for this). And keep track of maximum sum contiguous segment among all positive segments (max_so_far is used for this). Each time we get a positive sum compare it with max_so_far and update max_so_far if it is greater than max_so_far
Lets take the example:
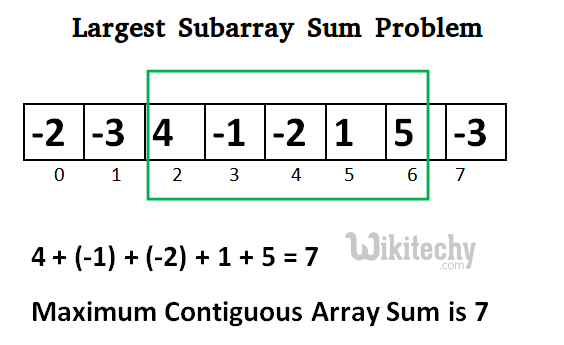
{-2, -3, 4, -1, -2, 1, 5, -3}
max_so_far = max_ending_here = 0
for i=0, a[0] = -2
max_ending_here = max_ending_here + (-2)
Set max_ending_here = 0 because max_ending_here < 0
for i=1, a[1] = -3
max_ending_here = max_ending_here + (-3)
Set max_ending_here = 0 because max_ending_here < 0
for i=2, a[2] = 4
max_ending_here = max_ending_here + (4)
max_ending_here = 4
max_so_far is updated to 4 because max_ending_here greater
than max_so_far which was 0 till now
for i=3, a[3] = -1
max_ending_here = max_ending_here + (-1)
max_ending_here = 3
for i=4, a[4] = -2
max_ending_here = max_ending_here + (-2)
max_ending_here = 1
for i=5, a[5] = 1
max_ending_here = max_ending_here + (1)
max_ending_here = 2
for i=6, a[6] = 5
max_ending_here = max_ending_here + (5)
max_ending_here = 7
max_so_far is updated to 7 because max_ending_here is
greater than max_so_far
for i=7, a[7] = -3
max_ending_here = max_ending_here + (-3)
max_ending_here = 4
[ad type=”banner”]
Program for Largest Sum Contiguous Subarray
[pastacode lang=”python” manual=”%0A%23%20Python%20program%20to%20find%20maximum%20contiguous%20subarray%20%0A%20%20%20%0A%23%20Function%20to%20find%20the%20maximum%20contiguous%20subarray%20%0Afrom%20sys%20import%20maxint%20%0Adef%20maxSubArraySum(a%2Csize)%3A%20%0A%20%20%20%20%20%20%20%0A%20%20%20%20max_so_far%20%3D%20-maxint%20-%201%0A%20%20%20%20max_ending_here%20%3D%200%0A%20%20%20%20%20%20%20%0A%20%20%20%20for%20i%20in%20range(0%2C%20size)%3A%20%0A%20%20%20%20%20%20%20%20max_ending_here%20%3D%20max_ending_here%20%2B%20a%5Bi%5D%20%0A%20%20%20%20%20%20%20%20if%20(max_so_far%20%3C%20max_ending_here)%3A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20max_so_far%20%3D%20max_ending_here%20%0A%20%20%0A%20%20%20%20%20%20%20%20if%20max_ending_here%20%3C%200%3A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20max_ending_here%20%3D%200%20%20%20%0A%20%20%20%20return%20max_so_far%20%0A%20%20%20%0A%23%20Driver%20function%20to%20check%20the%20above%20function%20%20%0Aa%20%3D%20%5B-13%2C%20-3%2C%20-25%2C%20-20%2C%20-3%2C%20-16%2C%20-23%2C%20-12%2C%20-5%2C%20-22%2C%20-15%2C%20-4%2C%20-7%5D%20%0Aprint%20%22Maximum%20contiguous%20sum%20is%22%2C%20maxSubArraySum(a%2Clen(a))%20″ message=”Python” highlight=”” provider=”manual”/]Output :
Maximum contiguous sum is -3
Above program can be optimized further, if we compare max_so_far with max_ending_here only if max_ending_here is greater than 0.
Program
[pastacode lang=”python” manual=”%0Adef%20maxSubArraySum(a%2Csize)%3A%20%0A%20%20%20%20%20%20%0A%20%20%20%20max_so_far%20%3D%200%0A%20%20%20%20max_ending_here%20%3D%200%0A%20%20%20%20%20%20%0A%20%20%20%20for%20i%20in%20range(0%2C%20size)%3A%20%0A%20%20%20%20%20%20%20%20max_ending_here%20%3D%20max_ending_here%20%2B%20a%5Bi%5D%20%0A%20%20%20%20%20%20%20%20if%20max_ending_here%20%3C%200%3A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20max_ending_here%20%3D%200%0A%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%23%20Do%20not%20compare%20for%20all%20elements.%20Compare%20only%20%20%20%20%0A%20%20%20%20%20%20%20%20%23%20when%20%20max_ending_here%20%3E%200%20%0A%20%20%20%20%20%20%20%20elif%20(max_so_far%20%3C%20max_ending_here)%3A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20max_so_far%20%3D%20max_ending_here%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20return%20max_so_far%20″ message=”Python” highlight=”” provider=”manual”/]Time Complexity: O(n)
Algorithmic Paradigm: Dynamic Programming
The implementation handles the case when all numbers in array are negative.
Program
[pastacode lang=”python” manual=”%0A%23%20Python%20program%20to%20find%20maximum%20contiguous%20subarray%20%0A%20%20%0Adef%20maxSubArraySum(a%2Csize)%3A%20%0A%20%20%20%20%20%20%0A%20%20%20%20max_so_far%20%3Da%5B0%5D%20%0A%20%20%20%20curr_max%20%3D%20a%5B0%5D%20%0A%20%20%20%20%20%20%0A%20%20%20%20for%20i%20in%20range(1%2Csize)%3A%20%0A%20%20%20%20%20%20%20%20curr_max%20%3D%20max(a%5Bi%5D%2C%20curr_max%20%2B%20a%5Bi%5D)%20%0A%20%20%20%20%20%20%20%20max_so_far%20%3D%20max(max_so_far%2Ccurr_max)%20%0A%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20return%20max_so_far%20%0A%20%20%0A%23%20Driver%20function%20to%20check%20the%20above%20function%20%20%0Aa%20%3D%20%5B-2%2C%20-3%2C%204%2C%20-1%2C%20-2%2C%201%2C%205%2C%20-3%5D%20%0Aprint%22Maximum%20contiguous%20sum%20is%22%20%2C%20maxSubArraySum(a%2Clen(a))%20″ message=”Python” highlight=”” provider=”manual”/]Output :
Maximum contiguous sum is 7
To print the subarray with the maximum sum, we maintain indices whenever we get the maximum sum.
Program
[pastacode lang=”python” manual=”%23%20Python%20program%20to%20print%20largest%20contiguous%20array%20sum%20%0A%20%20%0Afrom%20sys%20import%20maxsize%20%0A%20%20%0A%23%20Function%20to%20find%20the%20maximum%20contiguous%20subarray%20%0A%23%20and%20print%20its%20starting%20and%20end%20index%20%0Adef%20maxSubArraySum(a%2Csize)%3A%20%0A%20%20%0A%20%20%20%20max_so_far%20%3D%20-maxsize%20-%201%0A%20%20%20%20max_ending_here%20%3D%200%0A%20%20%20%20start%20%3D%200%0A%20%20%20%20end%20%3D%200%0A%20%20%20%20s%20%3D%200%0A%20%20%0A%20%20%20%20for%20i%20in%20range(0%2Csize)%3A%20%0A%20%20%0A%20%20%20%20%20%20%20%20max_ending_here%20%2B%3D%20a%5Bi%5D%20%0A%20%20%0A%20%20%20%20%20%20%20%20if%20max_so_far%20%3C%20max_ending_here%3A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20max_so_far%20%3D%20max_ending_here%20%0A%20%20%20%20%20%20%20%20%20%20%20%20start%20%3D%20s%20%0A%20%20%20%20%20%20%20%20%20%20%20%20end%20%3D%20i%20%0A%20%20%0A%20%20%20%20%20%20%20%20if%20max_ending_here%20%3C%200%3A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20max_ending_here%20%3D%200%0A%20%20%20%20%20%20%20%20%20%20%20%20s%20%3D%20i%2B1%0A%20%20%0A%20%20%20%20print%20(%22Maximum%20contiguous%20sum%20is%20%25d%22%25(max_so_far))%20%0A%20%20%20%20print%20(%22Starting%20Index%20%25d%22%25(start))%20%0A%20%20%20%20print%20(%22Ending%20Index%20%25d%22%25(end))%20%0A%20%20%0A%23%20Driver%20program%20to%20test%20maxSubArraySum%20%0Aa%20%3D%20%5B-2%2C%20-3%2C%204%2C%20-1%2C%20-2%2C%201%2C%205%2C%20-3%5D%20%0AmaxSubArraySum(a%2Clen(a))%20″ message=”Python” highlight=”” provider=”manual”/] [ad type=”banner”]Output :
Maximum contiguous sum is 7 Starting index 2 Ending index 6