Python Algorithm – Infix to Postfix Conversion using Stack

Infix expression:

• The expression of the form a op b. When an operator is in-between every pair of operands.

Postfix expression:

• The expression of the form a b op. When an operator is followed for every pair of operands.

Why postfix representation of the expression?

• The compiler scans the expression either from left to right or from right to left.

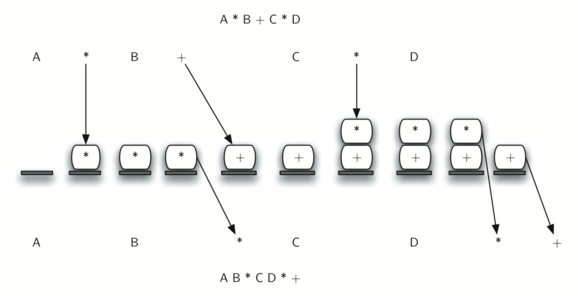
Consider the below expression:

a op1 b op2 c op3 d
If op1 = +, op2 = *, op3 = +

The compiler first scans the expression to evaluate the expression b * c, then again scan the expression to add a to it. The result is then added to d after another scan.

The repeated scanning makes it very in-efficient. It is better to convert the expression to postfix(or prefix) form before evaluation.

The corresponding expression in postfix form is: abc*+d+. The postfix expressions can be evaluated easily using a stack. We will cover postfix expression evaluation in a separate post.

[ad type=”banner”]

Algorithm

1. Scan the infix expression from left to right.
2. If the scanned character is an operand, output it.
3. Else,
—->3.1 If the precedence of the scanned operator is greater than the precedence of the operator in the stack(or the stack is empty), push it.
—–>3.2 Else, Pop the operator from the stack until the precedence of the scanned operator is less-equal to the precedence of the operator residing on the top of the stack. Push the scanned operator to the stack.
4. If the scanned character is an ‘(‘, push it to the stack.
5. If the scanned character is an ‘)’, pop and output from the stack until an ‘(‘ is encountered.
6. Repeat steps 2-6 until infix expression is scanned.
7. Pop and output from the stack until it is not empty.

Following is C implementation of the above algorithm

Python Programming:

[pastacode lang=”python” manual=”%23%20Python%20program%20to%20convert%20infix%20expression%20to%20postfix%0A%20%0A%23%20Class%20to%20convert%20the%20expression%0Aclass%20Conversion%3A%0A%20%20%20%20%20%0A%20%20%20%20%23%20Constructor%20to%20initialize%20the%20class%20variables%0A%20%20%20%20def%20__init__(self%2C%20capacity)%3A%0A%20%20%20%20%20%20%20%20self.top%20%3D%20-1%0A%20%20%20%20%20%20%20%20self.capacity%20%3D%20capacity%0A%20%20%20%20%20%20%20%20%23%20This%20array%20is%20used%20a%20stack%20%0A%20%20%20%20%20%20%20%20self.array%20%3D%20%5B%5D%0A%20%20%20%20%20%20%20%20%23%20Precedence%20setting%0A%20%20%20%20%20%20%20%20self.output%20%3D%20%5B%5D%0A%20%20%20%20%20%20%20%20self.precedence%20%3D%20%7B’%2B’%3A1%2C%20′-‘%3A1%2C%20’*’%3A2%2C%20’%2F’%3A2%2C%20’%5E’%3A3%7D%0A%20%20%20%20%20%0A%20%20%20%20%23%20check%20if%20the%20stack%20is%20empty%0A%20%20%20%20def%20isEmpty(self)%3A%0A%20%20%20%20%20%20%20%20return%20True%20if%20self.top%20%3D%3D%20-1%20else%20False%0A%20%20%20%20%20%0A%20%20%20%20%23%20Return%20the%20value%20of%20the%20top%20of%20the%20stack%0A%20%20%20%20def%20peek(self)%3A%0A%20%20%20%20%20%20%20%20return%20self.array%5B-1%5D%0A%20%20%20%20%20%0A%20%20%20%20%23%20Pop%20the%20element%20from%20the%20stack%0A%20%20%20%20def%20pop(self)%3A%0A%20%20%20%20%20%20%20%20if%20not%20self.isEmpty()%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20self.top%20-%3D%201%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20self.array.pop()%0A%20%20%20%20%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20%22%24%22%0A%20%20%20%20%20%0A%20%20%20%20%23%20Push%20the%20element%20to%20the%20stack%0A%20%20%20%20def%20push(self%2C%20op)%3A%0A%20%20%20%20%20%20%20%20self.top%20%2B%3D%201%0A%20%20%20%20%20%20%20%20self.array.append(op)%20%0A%20%0A%20%20%20%20%23%20A%20utility%20function%20to%20check%20is%20the%20given%20character%0A%20%20%20%20%23%20is%20operand%20%0A%20%20%20%20def%20isOperand(self%2C%20ch)%3A%0A%20%20%20%20%20%20%20%20return%20ch.isalpha()%0A%20%0A%20%20%20%20%23%20Check%20if%20the%20precedence%20of%20operator%20is%20strictly%0A%20%20%20%20%23%20less%20than%20top%20of%20stack%20or%20not%0A%20%20%20%20def%20notGreater(self%2C%20i)%3A%0A%20%20%20%20%20%20%20%20try%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20a%20%3D%20self.precedence%5Bi%5D%0A%20%20%20%20%20%20%20%20%20%20%20%20b%20%3D%20self.precedence%5Bself.peek()%5D%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20True%20if%20a%20%20%3C%3D%20b%20else%20False%0A%20%20%20%20%20%20%20%20except%20KeyError%3A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20False%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%23%20The%20main%20function%20that%20converts%20given%20infix%20expression%0A%20%20%20%20%23%20to%20postfix%20expression%0A%20%20%20%20def%20infixToPostfix(self%2C%20exp)%3A%0A%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%23%20Iterate%20over%20the%20expression%20for%20conversion%0A%20%20%20%20%20%20%20%20for%20i%20in%20exp%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%23%20If%20the%20character%20is%20an%20operand%2C%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%23%20add%20it%20to%20output%0A%20%20%20%20%20%20%20%20%20%20%20%20if%20self.isOperand(i)%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20self.output.append(i)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%23%20If%20the%20character%20is%20an%20′(‘%2C%20push%20it%20to%20stack%0A%20%20%20%20%20%20%20%20%20%20%20%20elif%20i%20%20%3D%3D%20′(‘%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20self.push(i)%0A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%23%20If%20the%20scanned%20character%20is%20an%20’)’%2C%20pop%20and%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%23%20output%20from%20the%20stack%20until%20and%20′(‘%20is%20found%0A%20%20%20%20%20%20%20%20%20%20%20%20elif%20i%20%3D%3D%20’)’%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20while(%20(not%20self.isEmpty())%20and%20self.peek()%20!%3D%20′(‘)%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20a%20%3D%20self.pop()%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20self.output.append(a)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(not%20self.isEmpty()%20and%20self.peek()%20!%3D%20′(‘)%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20return%20-1%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20self.pop()%0A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%23%20An%20operator%20is%20encountered%0A%20%20%20%20%20%20%20%20%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20while(not%20self.isEmpty()%20and%20self.notGreater(i))%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20self.output.append(self.pop())%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20self.push(i)%0A%20%0A%20%20%20%20%20%20%20%20%23%20pop%20all%20the%20operator%20from%20the%20stack%0A%20%20%20%20%20%20%20%20while%20not%20self.isEmpty()%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20self.output.append(self.pop())%0A%20%0A%20%20%20%20%20%20%20%20print%20%22%22.join(self.output)%0A%20%0A%23%20Driver%20program%20to%20test%20above%20function%0Aexp%20%3D%20%22a%2Bb*(c%5Ed-e)%5E(f%2Bg*h)-i%22%0Aobj%20%3D%20Conversion(len(exp))%0Aobj.infixToPostfix(exp)%0A%20%0A%23%20This%20code%20is%20contributed%20by%20Nikhil%20Kumar%20Singh(nickzuck_007)” message=”” highlight=”” provider=”manual”/] [ad type=”banner”]

Output:

abcd^e-fgh*+^*+i-