We have discussed a simple iterative postorder traversal using two stacks in the previous post. In this post, an approach with only one stack is discussed.
The idea is to move down to leftmost node using left pointer. While moving down, push root and root’s right child to stack. Once we reach leftmost node, print it if it doesn’t have a right child. If it has a right child, then change root so that the right child is processed before.
Following is detailed algorithm.
1.1 Create an empty stack
2.1 Do following while root is not NULL
a) Push root's right child and then root to stack.
b) Set root as root's left child.
2.2 Pop an item from stack and set it as root.
a) If the popped item has a right child and the right child
is at top of stack, then remove the right child from stack,
push the root back and set root as root's right child.
b) Else print root's data and set root as NULL.
2.3 Repeat steps 2.1 and 2.2 while stack is not empty.
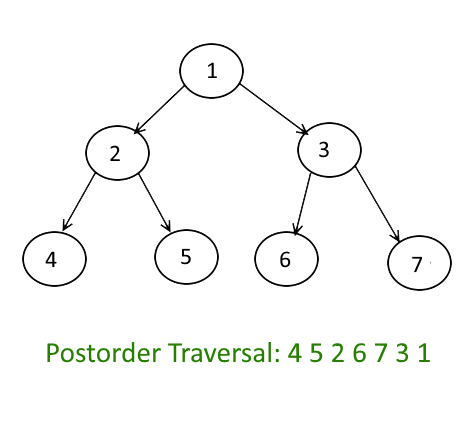
Let us consider the following tree
Following are the steps to print postorder traversal of the above tree using one stack.
1. Right child of 1 exists.
Push 3 to stack. Push 1 to stack. Move to left child.
Stack: 3, 1
2. Right child of 2 exists.
Push 5 to stack. Push 2 to stack. Move to left child.
Stack: 3, 1, 5, 2
3. Right child of 4 doesn't exist. '
Push 4 to stack. Move to left child.
Stack: 3, 1, 5, 2, 4
4. Current node is NULL.
Pop 4 from stack. Right child of 4 doesn't exist.
Print 4. Set current node to NULL.
Stack: 3, 1, 5, 2
5. Current node is NULL.
Pop 2 from stack. Since right child of 2 equals stack top element,
pop 5 from stack. Now push 2 to stack.
Move current node to right child of 2 i.e. 5
Stack: 3, 1, 2
6. Right child of 5 doesn't exist. Push 5 to stack. Move to left child.
Stack: 3, 1, 2, 5
7. Current node is NULL. Pop 5 from stack. Right child of 5 doesn't exist.
Print 5. Set current node to NULL.
Stack: 3, 1, 2
8. Current node is NULL. Pop 2 from stack.
Right child of 2 is not equal to stack top element.
Print 2. Set current node to NULL.
Stack: 3, 1
9. Current node is NULL. Pop 1 from stack.
Since right child of 1 equals stack top element, pop 3 from stack.
Now push 1 to stack. Move current node to right child of 1 i.e. 3
Stack: 1
10. Repeat the same as above steps and Print 6, 7 and 3.
Pop 1 and Print 1.
C Programming:
[pastacode lang=”c” manual=”%2F%2F%20C%20program%20for%20iterative%20postorder%20traversal%20using%20one%20stack%0A%23include%20%3Cstdio.h%3E%0A%23include%20%3Cstdlib.h%3E%0A%20%0A%2F%2F%20Maximum%20stack%20size%0A%23define%20MAX_SIZE%20100%0A%20%0A%2F%2F%20A%20tree%20node%0Astruct%20Node%0A%7B%0A%20%20%20%20int%20data%3B%0A%20%20%20%20struct%20Node%20*left%2C%20*right%3B%0A%7D%3B%0A%20%0A%2F%2F%20Stack%20type%0Astruct%20Stack%0A%7B%0A%20%20%20%20int%20size%3B%0A%20%20%20%20int%20top%3B%0A%20%20%20%20struct%20Node*%20*array%3B%0A%7D%3B%0A%20%0A%2F%2F%20A%20utility%20function%20to%20create%20a%20new%20tree%20node%0Astruct%20Node*%20newNode(int%20data)%0A%7B%0A%20%20%20%20struct%20Node*%20node%20%3D%20(struct%20Node*)%20malloc(sizeof(struct%20Node))%3B%0A%20%20%20%20node-%3Edata%20%3D%20data%3B%0A%20%20%20%20node-%3Eleft%20%3D%20node-%3Eright%20%3D%20NULL%3B%0A%20%20%20%20return%20node%3B%0A%7D%0A%20%0A%2F%2F%20A%20utility%20function%20to%20create%20a%20stack%20of%20given%20size%0Astruct%20Stack*%20createStack(int%20size)%0A%7B%0A%20%20%20%20struct%20Stack*%20stack%20%3D%20(struct%20Stack*)%20malloc(sizeof(struct%20Stack))%3B%0A%20%20%20%20stack-%3Esize%20%3D%20size%3B%0A%20%20%20%20stack-%3Etop%20%3D%20-1%3B%0A%20%20%20%20stack-%3Earray%20%3D%20(struct%20Node**)%20malloc(stack-%3Esize%20*%20sizeof(struct%20Node*))%3B%0A%20%20%20%20return%20stack%3B%0A%7D%0A%20%0A%2F%2F%20BASIC%20OPERATIONS%20OF%20STACK%0Aint%20isFull(struct%20Stack*%20stack)%0A%7B%20%20return%20stack-%3Etop%20-%201%20%3D%3D%20stack-%3Esize%3B%20%7D%0A%20%0Aint%20isEmpty(struct%20Stack*%20stack)%0A%7B%20%20return%20stack-%3Etop%20%3D%3D%20-1%3B%20%7D%0A%20%0Avoid%20push(struct%20Stack*%20stack%2C%20struct%20Node*%20node)%0A%7B%0A%20%20%20%20if%20(isFull(stack))%0A%20%20%20%20%20%20%20%20return%3B%0A%20%20%20%20stack-%3Earray%5B%2B%2Bstack-%3Etop%5D%20%3D%20node%3B%0A%7D%0A%20%0Astruct%20Node*%20pop(struct%20Stack*%20stack)%0A%7B%0A%20%20%20%20if%20(isEmpty(stack))%0A%20%20%20%20%20%20%20%20return%20NULL%3B%0A%20%20%20%20return%20stack-%3Earray%5Bstack-%3Etop–%5D%3B%0A%7D%0A%20%0Astruct%20Node*%20peek(struct%20Stack*%20stack)%0A%7B%0A%20%20%20%20if%20(isEmpty(stack))%0A%20%20%20%20%20%20%20%20return%20NULL%3B%0A%20%20%20%20return%20stack-%3Earray%5Bstack-%3Etop%5D%3B%0A%7D%0A%20%0A%2F%2F%20An%20iterative%20function%20to%20do%20postorder%20traversal%20of%20a%20given%20binary%20tree%0Avoid%20postOrderIterative(struct%20Node*%20root)%0A%7B%0A%20%20%20%20%2F%2F%20Check%20for%20empty%20tree%0A%20%20%20%20if%20(root%20%3D%3D%20NULL)%0A%20%20%20%20%20%20%20%20return%3B%0A%20%20%20%20%20%0A%20%20%20%20struct%20Stack*%20stack%20%3D%20createStack(MAX_SIZE)%3B%0A%20%20%20%20do%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20Move%20to%20leftmost%20node%0A%20%20%20%20%20%20%20%20while%20(root)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20Push%20root’s%20right%20child%20and%20then%20root%20to%20stack.%0A%20%20%20%20%20%20%20%20%20%20%20%20if%20(root-%3Eright)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20push(stack%2C%20root-%3Eright)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20push(stack%2C%20root)%3B%0A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20Set%20root%20as%20root’s%20left%20child%20%20%0A%20%20%20%20%20%20%20%20%20%20%20%20root%20%3D%20root-%3Eleft%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%0A%20%20%20%20%20%20%20%20%2F%2F%20Pop%20an%20item%20from%20stack%20and%20set%20it%20as%20root%20%20%20%20%0A%20%20%20%20%20%20%20%20root%20%3D%20pop(stack)%3B%0A%20%0A%20%20%20%20%20%20%20%20%2F%2F%20If%20the%20popped%20item%20has%20a%20right%20child%20and%20the%20right%20child%20is%20not%0A%20%20%20%20%20%20%20%20%2F%2F%20processed%20yet%2C%20then%20make%20sure%20right%20child%20is%20processed%20before%20root%0A%20%20%20%20%20%20%20%20if%20(root-%3Eright%20%26%26%20peek(stack)%20%3D%3D%20root-%3Eright)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20pop(stack)%3B%20%20%2F%2F%20remove%20right%20child%20from%20stack%0A%20%20%20%20%20%20%20%20%20%20%20%20push(stack%2C%20root)%3B%20%20%2F%2F%20push%20root%20back%20to%20stack%0A%20%20%20%20%20%20%20%20%20%20%20%20root%20%3D%20root-%3Eright%3B%20%2F%2F%20change%20root%20so%20that%20the%20right%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20child%20is%20processed%20next%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20else%20%20%2F%2F%20Else%20print%20root’s%20data%20and%20set%20root%20as%20NULL%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20printf(%22%25d%20%22%2C%20root-%3Edata)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20root%20%3D%20NULL%3B%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%7D%20while%20(!isEmpty(stack))%3B%0A%7D%0A%20%0A%2F%2F%20Driver%20program%20to%20test%20above%20functions%0Aint%20main()%0A%7B%0A%20%20%20%20%2F%2F%20Let%20us%20construct%20the%20tree%20shown%20in%20above%20figure%0A%20%20%20%20struct%20Node*%20root%20%3D%20NULL%3B%0A%20%20%20%20root%20%3D%20newNode(1)%3B%0A%20%20%20%20root-%3Eleft%20%3D%20newNode(2)%3B%0A%20%20%20%20root-%3Eright%20%3D%20newNode(3)%3B%0A%20%20%20%20root-%3Eleft-%3Eleft%20%3D%20newNode(4)%3B%0A%20%20%20%20root-%3Eleft-%3Eright%20%3D%20newNode(5)%3B%0A%20%20%20%20root-%3Eright-%3Eleft%20%3D%20newNode(6)%3B%0A%20%20%20%20root-%3Eright-%3Eright%20%3D%20newNode(7)%3B%0A%20%20%20%20printf(%22Post%20order%20traversal%20of%20binary%20tree%20is%20%3A%5Cn%22)%3B%0A%20%20%20%20printf(%22%5B%22)%3B%0A%20%20%20%20postOrderIterative(root)%3B%0A%20%20%20%20printf(%22%5D%22)%3B%0A%20%20%20%20%20%0A%20%0A%20%20%20%20return%200%3B%0A%7D” message=”” highlight=”” provider=”manual”/]Output:
Post Order traversal of binary tree is [4, 5, 2, 6, 7, 3, 1]