Given a directed and two vertices ‘u’ and ‘v’ in it, find shortest path from ‘u’ to ‘v’ with exactly k edges on the path.
The graph is given as adjacency matrix representation where value of graph[i][j] indicates the weight of an edge from vertex i to vertex j and a value INF(infinite) indicates no edge from i to j.
For example consider the following graph. Let source ‘u’ be vertex 0, destination ‘v’ be 3 and k be 2. There are two walks of length 2, the walks are {0, 2, 3} and {0, 1, 3}. The shortest among the two is {0, 2, 3} and weight of path is 3+6 = 9.
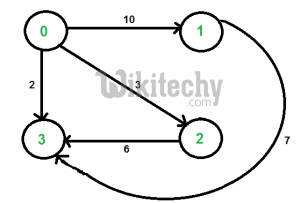
The idea is to browse through all paths of length k from u to v using the approach discussed in the previous post and return weight of the shortest path. A simple solution is to start from u, go to all adjacent vertices and recur for adjacent vertices with k as k-1, source as adjacent vertex and destination as v. Following are C++ and Java implementations of this simple solution.
[ad type=”banner”]Java Programming
[pastacode lang=”java” manual=”%2F%2F%20Dynamic%20Programming%20based%20Java%20program%20to%20find%20shortest%20path%0A%2F%2F%20with%20exactly%20k%20edges%0Aimport%20java.util.*%3B%0Aimport%20java.lang.*%3B%0Aimport%20java.io.*%3B%0A%20%0Aclass%20ShortestPath%0A%7B%0A%20%20%20%20%2F%2F%20Define%20number%20of%20vertices%20in%20the%20graph%20and%20inifinite%20value%0A%20%20%20%20static%20final%20int%20V%20%3D%204%3B%0A%20%20%20%20static%20final%20int%20INF%20%3D%20Integer.MAX_VALUE%3B%0A%20%0A%20%20%20%20%2F%2F%20A%20naive%20recursive%20function%20to%20count%20walks%20from%20u%20to%20v%0A%20%20%20%20%2F%2F%20with%20k%20edges%0A%20%20%20%20int%20shortestPath(int%20graph%5B%5D%5B%5D%2C%20int%20u%2C%20int%20v%2C%20int%20k)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20Base%20cases%0A%20%20%20%20%20%20%20%20if%20(k%20%3D%3D%200%20%26%26%20u%20%3D%3D%20v)%20%20%20%20%20%20%20%20%20%20%20%20%20return%200%3B%0A%20%20%20%20%20%20%20%20if%20(k%20%3D%3D%201%20%26%26%20graph%5Bu%5D%5Bv%5D%20!%3D%20INF)%20return%20graph%5Bu%5D%5Bv%5D%3B%0A%20%20%20%20%20%20%20%20if%20(k%20%3C%3D%200)%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20return%20INF%3B%0A%20%0A%20%20%20%20%20%20%20%20%2F%2F%20Initialize%20result%0A%20%20%20%20%20%20%20%20int%20res%20%3D%20INF%3B%0A%20%0A%20%20%20%20%20%20%20%20%2F%2F%20Go%20to%20all%20adjacents%20of%20u%20and%20recur%0A%20%20%20%20%20%20%20%20for%20(int%20i%20%3D%200%3B%20i%20%3C%20V%3B%20i%2B%2B)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20if%20(graph%5Bu%5D%5Bi%5D%20!%3D%20INF%20%26%26%20u%20!%3D%20i%20%26%26%20v%20!%3D%20i)%0A%20%20%20%20%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20int%20rec_res%20%3D%20shortestPath(graph%2C%20i%2C%20v%2C%20k-1)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(rec_res%20!%3D%20INF)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20res%20%3D%20Math.min(res%2C%20graph%5Bu%5D%5Bi%5D%20%2B%20rec_res)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20return%20res%3B%0A%20%20%20%20%7D%0A%20%0A%20%20%20%20public%20static%20void%20main%20(String%5B%5D%20args)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F*%20Let%20us%20create%20the%20graph%20shown%20in%20above%20diagram*%2F%0A%20%20%20%20%20%20%20%20int%20graph%5B%5D%5B%5D%20%3D%20new%20int%5B%5D%5B%5D%7B%20%7B0%2C%2010%2C%203%2C%202%7D%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7BINF%2C%200%2C%20INF%2C%207%7D%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7BINF%2C%20INF%2C%200%2C%206%7D%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7BINF%2C%20INF%2C%20INF%2C%200%7D%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7D%3B%0A%20%20%20%20%20%20%20%20ShortestPath%20t%20%3D%20new%20ShortestPath()%3B%0A%20%20%20%20%20%20%20%20int%20u%20%3D%200%2C%20v%20%3D%203%2C%20k%20%3D%202%3B%0A%20%20%20%20%20%20%20%20System.out.println(%22Weight%20of%20the%20shortest%20path%20is%20%22%2B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20t.shortestPath(graph%2C%20u%2C%20v%2C%20k))%3B%0A%20%20%20%20%7D%0A%7D” message=”” highlight=”” provider=”manual”/]Output:
Weight of the shortest path is 9
The worst case time complexity of the above function is O(Vk) where V is the number of vertices in the given graph. We can simply analyze the time complexity by drawing recursion tree. The worst occurs for a complete graph. In worst case, every internal node of recursion tree would have exactly V children.
We can optimize the above solution using Dynamic Programming. The idea is to build a 3D table where first dimension is source, second dimension is destination, third dimension is number of edges from source to destination, and the value is count of walks. Like other Dynamic Programming problems, we fill the 3D table in bottom up manner.
Java programming
[pastacode lang=”java” manual=”%2F%2F%20Dynamic%20Programming%20based%20Java%20program%20to%20find%20shortest%20path%20with%0A%2F%2F%20exactly%20k%20edges%0Aimport%20java.util.*%3B%0Aimport%20java.lang.*%3B%0Aimport%20java.io.*%3B%0A%20%0Aclass%20ShortestPath%0A%7B%0A%20%20%20%20%2F%2F%20Define%20number%20of%20vertices%20in%20the%20graph%20and%20inifinite%20value%0A%20%20%20%20static%20final%20int%20V%20%3D%204%3B%0A%20%20%20%20static%20final%20int%20INF%20%3D%20Integer.MAX_VALUE%3B%0A%20%0A%20%20%20%20%2F%2F%20A%20Dynamic%20programming%20based%20function%20to%20find%20the%20shortest%20path%0A%20%20%20%20%2F%2F%20from%20u%20to%20v%20with%20exactly%20k%20edges.%0A%20%20%20%20int%20shortestPath(int%20graph%5B%5D%5B%5D%2C%20int%20u%2C%20int%20v%2C%20int%20k)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F%2F%20Table%20to%20be%20filled%20up%20using%20DP.%20The%20value%20sp%5Bi%5D%5Bj%5D%5Be%5D%20will%0A%20%20%20%20%20%20%20%20%2F%2F%20store%20weight%20of%20the%20shortest%20path%20from%20i%20to%20j%20with%20exactly%0A%20%20%20%20%20%20%20%20%2F%2F%20k%20edges%0A%20%20%20%20%20%20%20%20int%20sp%5B%5D%5B%5D%5B%5D%20%3D%20new%20int%5BV%5D%5BV%5D%5Bk%2B1%5D%3B%0A%20%0A%20%20%20%20%20%20%20%20%2F%2F%20Loop%20for%20number%20of%20edges%20from%200%20to%20k%0A%20%20%20%20%20%20%20%20for%20(int%20e%20%3D%200%3B%20e%20%3C%3D%20k%3B%20e%2B%2B)%0A%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20for%20(int%20i%20%3D%200%3B%20i%20%3C%20V%3B%20i%2B%2B)%20%20%2F%2F%20for%20source%0A%20%20%20%20%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20for%20(int%20j%20%3D%200%3B%20j%20%3C%20V%3B%20j%2B%2B)%20%2F%2F%20for%20destination%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20initialize%20value%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20sp%5Bi%5D%5Bj%5D%5Be%5D%20%3D%20INF%3B%0A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20from%20base%20cases%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(e%20%3D%3D%200%20%26%26%20i%20%3D%3D%20j)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20sp%5Bi%5D%5Bj%5D%5Be%5D%20%3D%200%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(e%20%3D%3D%201%20%26%26%20graph%5Bi%5D%5Bj%5D%20!%3D%20INF)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20sp%5Bi%5D%5Bj%5D%5Be%5D%20%3D%20graph%5Bi%5D%5Bj%5D%3B%0A%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20go%20to%20adjacent%20only%20when%20number%20of%20edges%20is%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20more%20than%201%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(e%20%3E%201)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20for%20(int%20a%20%3D%200%3B%20a%20%3C%20V%3B%20a%2B%2B)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20There%20should%20be%20an%20edge%20from%20i%20to%20a%20and%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%2F%2F%20a%20should%20not%20be%20same%20as%20either%20i%20or%20j%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20(graph%5Bi%5D%5Ba%5D%20!%3D%20INF%20%26%26%20i%20!%3D%20a%20%26%26%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20j!%3D%20a%20%26%26%20sp%5Ba%5D%5Bj%5D%5Be-1%5D%20!%3D%20INF)%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20sp%5Bi%5D%5Bj%5D%5Be%5D%20%3D%20Math.min(sp%5Bi%5D%5Bj%5D%5Be%5D%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20graph%5Bi%5D%5Ba%5D%20%2B%20sp%5Ba%5D%5Bj%5D%5Be-1%5D)%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20return%20sp%5Bu%5D%5Bv%5D%5Bk%5D%3B%0A%20%20%20%20%7D%0A%20%0A%20%20%20%20public%20static%20void%20main%20(String%5B%5D%20args)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20%2F*%20Let%20us%20create%20the%20graph%20shown%20in%20above%20diagram*%2F%0A%20%20%20%20%20%20%20%20int%20graph%5B%5D%5B%5D%20%3D%20new%20int%5B%5D%5B%5D%7B%20%7B0%2C%2010%2C%203%2C%202%7D%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7BINF%2C%200%2C%20INF%2C%207%7D%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7BINF%2C%20INF%2C%200%2C%206%7D%2C%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7BINF%2C%20INF%2C%20INF%2C%200%7D%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%7D%3B%0A%20%20%20%20%20%20%20%20ShortestPath%20t%20%3D%20new%20ShortestPath()%3B%0A%20%20%20%20%20%20%20%20int%20u%20%3D%200%2C%20v%20%3D%203%2C%20k%20%3D%202%3B%0A%20%20%20%20%20%20%20%20System.out.println(%22Weight%20of%20the%20shortest%20path%20is%20%22%2B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20t.shortestPath(graph%2C%20u%2C%20v%2C%20k))%3B%0A%20%20%20%20%7D%0A%7D” message=”” highlight=”” provider=”manual”/]Output:
Weight of the shortest path is 9[ad type=”banner”]