A disjoint-set data structure is a data structure that keeps track of a set of elements partitioned into a number of disjoint (non-overlapping) subsets. A union-find algorithm is an algorithm that performs two useful operations on such a data structure:
Find: Determine which subset a particular element is in. This can be used for determining if two elements are in the same subset.
Union: Join two subsets into a single subset.
In this post, we will discuss an application of Disjoint Set Data Structure. The application is to check whether a given graph contains a cycle or not.
Union-Find Algorithm can be used to check whether an undirected graph contains cycle or not. Note that we have discussed an algorithm to detect cycle. This is another method based on Union-Find. This method assumes that graph doesn’t contain any self-loops.
We can keeps track of the subsets in a 1D array, lets call it parent[].
Let us consider the following graph:
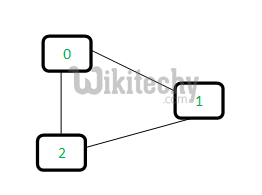
For each edge, make subsets using both the vertices of the edge. If both the vertices are in the same subset, a cycle is found.
Initially, all slots of parent array are initialized to -1 (means there is only one item in every subset).
0 1 2
-1 -1 -1
Now process all edges one by one.
Edge 0-1: Find the subsets in which vertices 0 and 1 are. Since they are in different subsets, we take the union of them. For taking the union, either make node 0 as parent of node 1 or vice-versa.
0 1 2 <----- 1 is made parent of 0 (1 is now representative of subset {0, 1})
1 -1 -1
Edge 1-2: 1 is in subset 1 and 2 is in subset 2. So, take union.
0 1 2 <----- 2 is made parent of 1 (2 is now representative of subset {0, 1, 2})
1 2 -1
Edge 0-2: 0 is in subset 2 and 2 is also in subset 2. Hence, including this edge forms a cycle.
How subset of 0 is same as 2?
0->1->2 // 1 is parent of 0 and 2 is parent of 1
Based on the above explanation, below are implementations:
// A union-find algorithm to detect cycle in a graph
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// a structure to represent an edge in graph
struct Edge
{
int src, dest;
};
// a structure to represent a graph
struct Graph
{
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges
struct Edge* edge;
};
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
struct Graph* graph =
(struct Graph*) malloc( sizeof(struct Graph) );
graph->V = V;
graph->E = E;
graph->edge =
(struct Edge*) malloc( graph->E * sizeof( struct Edge ) );
return graph;
}
// A utility function to find the subset of an element i
int find(int parent[], int i)
{
if (parent[i] == -1)
return i;
return find(parent, parent[i]);
}
// A utility function to do union of two subsets
void Union(int parent[], int x, int y)
{
int xset = find(parent, x);
int yset = find(parent, y);
parent[xset] = yset;
}
// The main function to check whether a given graph contains
// cycle or not
int isCycle( struct Graph* graph )
{
// Allocate memory for creating V subsets
int *parent = (int*) malloc( graph->V * sizeof(int) );
// Initialize all subsets as single element sets
memset(parent, -1, sizeof(int) * graph->V);
// Iterate through all edges of graph, find subset of both
// vertices of every edge, if both subsets are same, then
// there is cycle in graph.
for(int i = 0; i < graph->E; ++i)
{
int x = find(parent, graph->edge[i].src);
int y = find(parent, graph->edge[i].dest);
if (x == y)
return 1;
Union(parent, x, y);
}
return 0;
}
// Driver program to test above functions
int main()
{
/* Let us create following graph
0
| \
| \
1-----2 */
int V = 3, E = 3;
struct Graph* graph = createGraph(V, E);
// add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
// add edge 1-2
graph->edge[1].src = 1;
graph->edge[1].dest = 2;
// add edge 0-2
graph->edge[2].src = 0;
graph->edge[2].dest = 2;
if (isCycle(graph))
printf( "graph contains cycle" );
else
printf( "graph doesn't contain cycle" );
return 0;
}
Output:
graph contains cycle