A disjoint-set data structure is a data structure that keeps track of a set of elements partitioned into a number of disjoint (non-overlapping) subsets. A union-find algorithm is an algorithm that performs two useful operations on such a data structure:
Find: Determine which subset a particular element is in. This can be used for determining if two elements are in the same subset.
Union: Join two subsets into a single subset.
In this post, we will discuss an application of Disjoint Set Data Structure. The application is to check whether a given graph contains a cycle or not.
Union-Find Algorithm can be used to check whether an undirected graph contains cycle or not. Note that we have discussed an algorithm to detect cycle. This is another method based on Union-Find. This method assumes that graph doesn’t contain any self-loops.
We can keeps track of the subsets in a 1D array, lets call it parent[].
Let us consider the following graph:
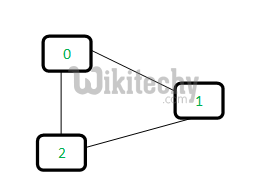
For each edge, make subsets using both the vertices of the edge. If both the vertices are in the same subset, a cycle is found.
Initially, all slots of parent array are initialized to -1 (means there is only one item in every subset).
0 1 2 -1 -1 -1
Now process all edges one by one.
Edge 0-1: Find the subsets in which vertices 0 and 1 are. Since they are in different subsets, we take the union of them. For taking the union, either make node 0 as parent of node 1 or vice-versa.
0 1 2 <----- 1 is made parent of 0 (1 is now representative of subset {0, 1})
1 -1 -1
Edge 1-2: 1 is in subset 1 and 2 is in subset 2. So, take union.
0 1 2 <----- 2 is made parent of 1 (2 is now representative of subset {0, 1, 2})
1 2 -1
Edge 0-2: 0 is in subset 2 and 2 is also in subset 2. Hence, including this edge forms a cycle.
How subset of 0 is same as 2?
0->1->2 // 1 is parent of 0 and 2 is parent of 1
Based on the above explanation, below are implementations:
Java Programming:
[pastacode lang=”java” manual=”%2F%2F%20A%20union-find%20algorithm%20to%20detect%20cycle%20in%20a%20graph%0A%23include%20%3Cstdio.h%3E%0A%23include%20%3Cstdlib.h%3E%0A%23include%20%3Cstring.h%3E%0A%20%0A%2F%2F%20a%20structure%20to%20represent%20an%20edge%20in%20graph%0Astruct%20Edge%0A%7B%0A%20%20%20%20int%20src%2C%20dest%3B%0A%7D%3B%0A%20%0A%2F%2F%20a%20structure%20to%20represent%20a%20graph%0Astruct%20Graph%0A%7B%0A%20%20%20%20%2F%2F%20V-%3E%20Number%20of%20vertices%2C%20E-%3E%20Number%20of%20edges%0A%20%20%20%20int%20V%2C%20E%3B%0A%20%0A%20%20%20%20%2F%2F%20graph%20is%20represented%20as%20an%20array%20of%20edges%0A%20%20%20%20struct%20Edge*%20edge%3B%0A%7D%3B%0A%20%0A%2F%2F%20Creates%20a%20graph%20with%20V%20vertices%20and%20E%20edges%0Astruct%20Graph*%20createGraph(int%20V%2C%20int%20E)%0A%7B%0A%20%20%20%20struct%20Graph*%20graph%20%3D%20%0A%20%20%20%20%20%20%20%20%20%20%20(struct%20Graph*)%20malloc(%20sizeof(struct%20Graph)%20)%3B%0A%20%20%20%20graph-%3EV%20%3D%20V%3B%0A%20%20%20%20graph-%3EE%20%3D%20E%3B%0A%20%0A%20%20%20%20graph-%3Eedge%20%3D%20%0A%20%20%20%20%20%20%20%20(struct%20Edge*)%20malloc(%20graph-%3EE%20*%20sizeof(%20struct%20Edge%20)%20)%3B%0A%20%0A%20%20%20%20return%20graph%3B%0A%7D%0A%20%0A%2F%2F%20A%20utility%20function%20to%20find%20the%20subset%20of%20an%20element%20i%0Aint%20find(int%20parent%5B%5D%2C%20int%20i)%0A%7B%0A%20%20%20%20if%20(parent%5Bi%5D%20%3D%3D%20-1)%0A%20%20%20%20%20%20%20%20return%20i%3B%0A%20%20%20%20return%20find(parent%2C%20parent%5Bi%5D)%3B%0A%7D%0A%20%0A%2F%2F%20A%20utility%20function%20to%20do%20union%20of%20two%20subsets%20%0Avoid%20Union(int%20parent%5B%5D%2C%20int%20x%2C%20int%20y)%0A%7B%0A%20%20%20%20int%20xset%20%3D%20find(parent%2C%20x)%3B%0A%20%20%20%20int%20yset%20%3D%20find(parent%2C%20y)%3B%0A%20%20%20%20parent%5Bxset%5D%20%3D%20yset%3B%0A%7D%0A%20%0A%2F%2F%20The%20main%20function%20to%20check%20whether%20a%20given%20graph%20contains%20%0A%2F%2F%20cycle%20or%20not%0Aint%20isCycle(%20struct%20Graph*%20graph%20)%0A%7B%0A%20%20%20%20%2F%2F%20Allocate%20memory%20for%20creating%20V%20subsets%0A%20%20%20%20int%20*parent%20%3D%20(int*)%20malloc(%20graph-%3EV%20*%20sizeof(int)%20)%3B%0A%20%0A%20%20%20%20%2F%2F%20Initialize%20all%20subsets%20as%20single%20element%20sets%0A%20%20%20%20memset(parent%2C%20-1%2C%20sizeof(int)%20*%20graph-%3EV)%3B%0A%20%0A%20%20%20%20%2F%2F%20Iterate%20through%20all%20edges%20of%20graph%2C%20find%20subset%20of%20both%0A%20%20%20%20%2F%2F%20vertices%20of%20every%20edge%2C%20if%20both%20subsets%20are%20same%2C%20then%20%0A%20%20%20%20%2F%2F%20there%20is%20cycle%20in%20graph.%0A%20%20%20%20for(int%20i%20%3D%200%3B%20i%20%3C%20graph-%3EE%3B%20%2B%2Bi)%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20int%20x%20%3D%20find(parent%2C%20graph-%3Eedge%5Bi%5D.src)%3B%0A%20%20%20%20%20%20%20%20int%20y%20%3D%20find(parent%2C%20graph-%3Eedge%5Bi%5D.dest)%3B%0A%20%0A%20%20%20%20%20%20%20%20if%20(x%20%3D%3D%20y)%0A%20%20%20%20%20%20%20%20%20%20%20%20return%201%3B%0A%20%0A%20%20%20%20%20%20%20%20Union(parent%2C%20x%2C%20y)%3B%0A%20%20%20%20%7D%0A%20%20%20%20return%200%3B%0A%7D%0A%20%0A%2F%2F%20Driver%20program%20to%20test%20above%20functions%0Aint%20main()%0A%7B%0A%20%20%20%20%2F*%20Let%20us%20create%20following%20graph%0A%20%20%20%20%20%20%20%20%200%0A%20%20%20%20%20%20%20%20%7C%20%20%5C%0A%20%20%20%20%20%20%20%20%7C%20%20%20%20%5C%0A%20%20%20%20%20%20%20%201—–2%20*%2F%20%20%20%20%0A%20%20%20%20int%20V%20%3D%203%2C%20E%20%3D%203%3B%0A%20%20%20%20struct%20Graph*%20graph%20%3D%20createGraph(V%2C%20E)%3B%0A%20%0A%20%20%20%20%2F%2F%20add%20edge%200-1%0A%20%20%20%20graph-%3Eedge%5B0%5D.src%20%3D%200%3B%0A%20%20%20%20graph-%3Eedge%5B0%5D.dest%20%3D%201%3B%0A%20%0A%20%20%20%20%2F%2F%20add%20edge%201-2%0A%20%20%20%20graph-%3Eedge%5B1%5D.src%20%3D%201%3B%0A%20%20%20%20graph-%3Eedge%5B1%5D.dest%20%3D%202%3B%0A%20%0A%20%20%20%20%2F%2F%20add%20edge%200-2%0A%20%20%20%20graph-%3Eedge%5B2%5D.src%20%3D%200%3B%0A%20%20%20%20graph-%3Eedge%5B2%5D.dest%20%3D%202%3B%0A%20%0A%20%20%20%20if%20(isCycle(graph))%0A%20%20%20%20%20%20%20%20printf(%20%22graph%20contains%20cycle%22%20)%3B%0A%20%20%20%20else%0A%20%20%20%20%20%20%20%20printf(%20%22graph%20doesn’t%20contain%20cycle%22%20)%3B%0A%20%0A%20%20%20%20return%200%3B%0A%7D” message=”” highlight=”” provider=”manual”/]Output:
graph contains cycle