Kruskal’s Minimum Spanning Tree using STL in C++
Given an undirected, connected and weighted graph, find Minimum Spanning Tree (MST) of the graph using Kruskal’s algorithm.

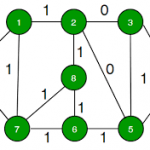
Input : Graph as an array of edges
Output : Edges of MST are
6 - 7
2 - 8
5 - 6
0 - 1
2 - 5
2 - 3
0 - 7
3 - 4
Weight of MST is 37
Note : There are two possible MSTs, the other
MST includes edge 1-2 in place of 0-7.
We have discussed below Kruskal’s MST implementations.
Greedy Algorithms | Set 2 (Kruskal’s Minimum Spanning Tree Algorithm)
Below are the steps for finding MST using Kruskal’s algorithm
- Sort all the edges in non-decreasing order of their weight.
- Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it.
- Repeat step#2 until there are (V-1) edges in the spanning tree.
Here are some key points which will be useful for us in implementing the Kruskal’s algorithm using STL.
- Use a vector of edges which consist of all the edges in the graph and each item of a vector will contain 3 parameters: source, destination and the cost of an edge between the source and destination.
vector<pair<int, pair<int, int> > > edges;
Here in the outer pair (i.e pair<int,pair<int,int> > ) the first element corresponds to the cost of a edge while the second element is itself a pair, and it contains two vertices of edge.
- Use the inbuilt std::sort to sort the edges in the non-decreasing order; by default the sort function sort in non-decreasing order.
- We use the Union Find Algorithm to check if it the current edge forms a cycle if it is added in the current MST. If yes discard it, else include it (union).
Pseudo Code:
// Initialize result
mst_weight = 0
// Create V single item sets
for each vertex v
parent[v] = v;
rank[v] = 0;
Sort all edges into non decreasing
order by weight w
for each (u, v) taken from the sorted list E
do if FIND-SET(u) != FIND-SET(v)
print edge(u, v)
mst_weight += weight of edge(u, v)
UNION(u, v)
Below is C++ implementation of above algorithm.
Output :
Edges of MST are
6 - 7
2 - 8
5 - 6
0 - 1
2 - 5
2 - 3
0 - 7
3 - 4
Weight of MST is 37